BA-DDG:引入非结合态+逆折叠模型计算PPI的互作自由能变化
Abstract
预测蛋白质-蛋白质相互作用中结合自由能的变化(ΔΔG)对于理解和调控这些相互作用至关重要,尤其在药物设计领域 。由于实验性的$\Delta\Delta G$数据稀缺,现有方法主要集中在预训练上,却忽略了“对齐”(alignment)的重要性 。在这项工作中,研究人员提出了一种名为玻尔兹曼对齐(Boltzmann Alignment)的技术,旨在将知识从预训练的逆折叠模型迁移到$\Delta\Delta G$的预测任务中。
他们首先分析了$\Delta\Delta G$的热力学定义,并引入玻尔兹曼分布,将能量与蛋白质的构象分布联系起来。然而,蛋白质的构象分布是难以直接处理的 。因此,他们运用贝叶斯定理来规避直接估算,转而利用蛋白质逆折叠模型提供的对数似然(log-likelihood)来估算$\Delta\Delta G$ 。与以往基于逆折叠模型的方法相比,该方法在$\Delta\Delta G$的热力学循环中显式地考虑了蛋白质复合物的非结合态(unbound state),从而引入了物理学的归纳偏置,并实现了在有监督和无监督两种设定下的当前最优(SoTA)性能 。
实验结果表明,在SKEMPI v2数据集上,该方法在无监督和有监督设定下分别取得了0.3201和0.5134的Spearman相关系数,显著超过了先前报道的最高纪录(分别为0.2632和0.4324) 。此外,作者还展示了该方法在结合能预测、蛋白质对接以及抗体优化等任务中的能力 。
1 Introduction
蛋白质-蛋白质相互作用(PPIs)是所有生物体中执行多样化和关键生物功能的基础 。对这些相互作用进行高保真的计算建模是不可或缺的 。蛋白质结合的特性可以通过结合自由能(ΔG)来定量表征,即结合态与非结合态之间吉布斯自由能的差异 。而预测结合自由能的变化(ΔΔG),也被称为突变效应,对于调控蛋白质间的相互作用至关重要 。准确预测 $\Delta\Delta G$ 能够帮助识别增强或减弱结合强度的突变,从而指导高效的蛋白质设计,加速治疗性干预措施的开发,并加深我们对生物学机制的理解 。
深度学习在蛋白质建模方面展现出巨大潜力,并引发了 $\Delta\Delta G$ 预测计算方法的范式转变。然而,尽管取得了进展,$\Delta\Delta G$预测任务仍然受到标注实验数据稀缺的严重制约 。因此,在大量无标签数据上进行预训练已成为一种主流策略 。最近的研究观察到,结构预测模型和逆折叠模型能隐式地捕捉蛋白质的能量分布 。
尽管基于预训练的方法是有效的,但它们仅仅采用监督微调(SFT)的方式,而忽略了“对齐”(alignment)的重要性 。监督微调可能会导致模型灾难性地遗忘其在无监督预训练阶段学到的通用知识,因此在知识迁移方面仍有提升空间 。在其他生物学任务中,已有研究借鉴了大型语言模型(LLM)的对齐技术,如直接偏好优化(DPO),来将实验适应性信息整合到生物生成模型中 。然而,作者指出,直接将这些对齐技术用于 $\Delta\Delta G$ 预测是不够的,因为它们缺乏与能量相关的生物学任务所需的物理归纳偏置(physical inductive bias) 。
为此,本文提出了一种名为玻尔兹曼对齐(Boltzmann Alignment)的新技术,旨在将知识从预训练的逆折叠模型迁移到$\Delta\Delta G$预测任务中 。
- 该方法首先分析了
$\Delta\Delta G$的热力学定义,并引入玻尔兹曼分布将能量与蛋白质构象分布联系起来,从而突出了预训练概率模型的潜力 。 - 由于蛋白质构象分布难以直接求解,作者运用贝叶斯定理来规避直接估算,转而利用蛋白质逆折叠模型提供的对数似然(log-likelihood)来进行
$\Delta\Delta G$的估算 。 - 这一推导为先前研究中观察到的“逆折叠模型输出的对数似然与结合能高度相关”的现象提供了合理的解释 。
- 与之前的逆折叠方法相比,该方法明确考虑了蛋白质复合物的非结合态,使得对逆折叠模型的微调方式与统计热力学保持一致 。
本文的贡献可总结为以下几点:
- 提出了玻尔兹曼对齐方法,通过玻尔兹曼分布和热力学循环引入物理归纳偏置,将预训练逆折叠模型的知识迁移到
$\Delta\Delta G$预测中 。 - 在SKEMPI v2数据集上的实验结果表明,该方法在无监督和有监督设定下均取得了当前最优(SOTA)的性能,Spearman相关系数分别达到了0.3201和0.5134,显著超越了之前报道的0.2632和0.4324 。
- 消融实验证明,该方法优于以往的基于逆折叠模型的方法以及其他的对齐技术 。
- 展示了该方法在结合能预测、蛋白质-蛋白质对接和抗体优化等更广泛任务中的应用潜力 。
3 Method
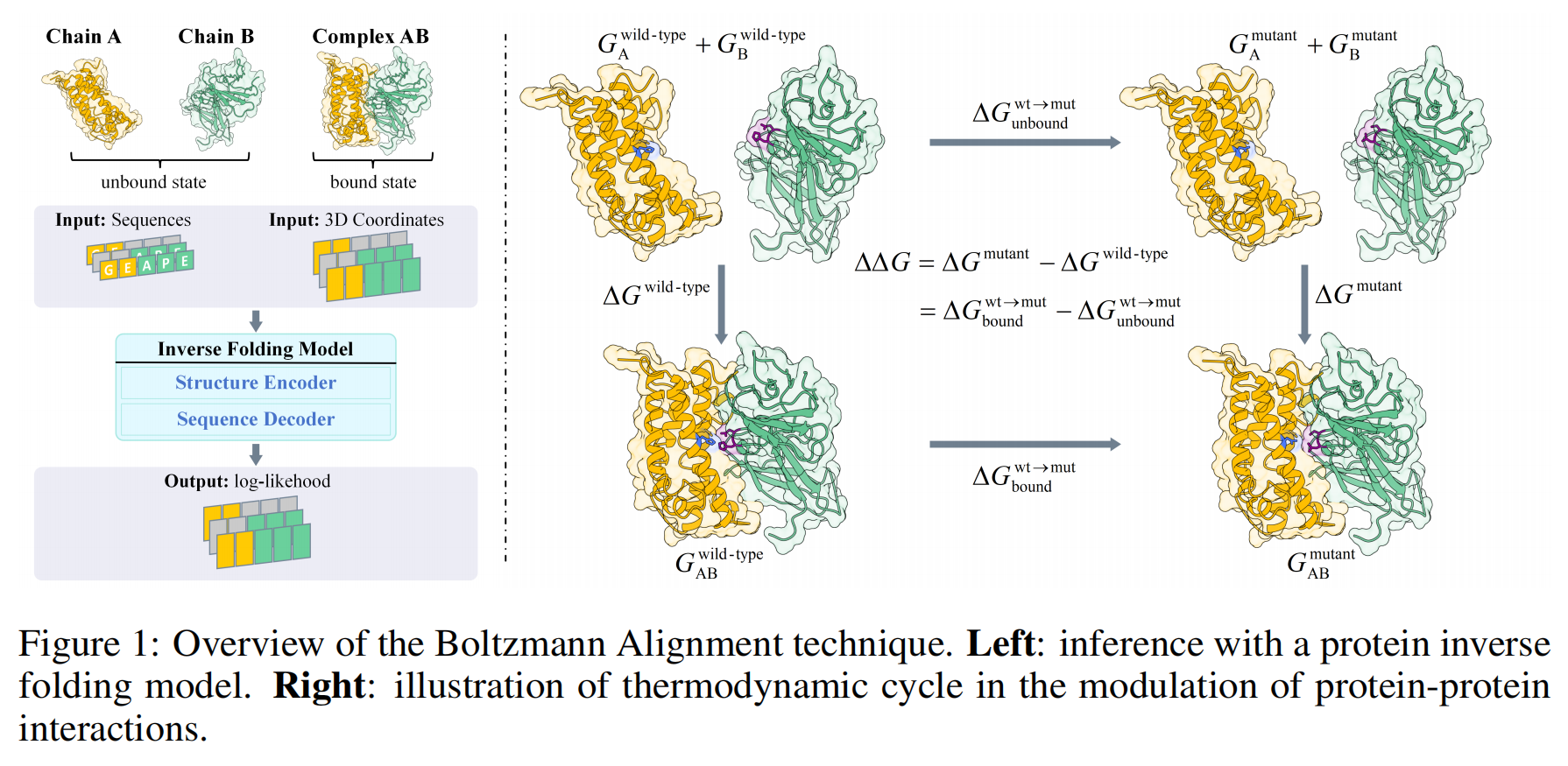
3.1 Blotzmann Alignment
对于一个由链A和链B组成的复合物,其结合自由能 $\Delta G$ 是结合态(boundstate)的吉布斯自由能 $G_{bnd}$ 与非结合态(unboundstate)的吉布斯自由能 $G_{unbnd}$ 之差。根据玻尔兹曼分布,$\Delta G$ 可以表示为:
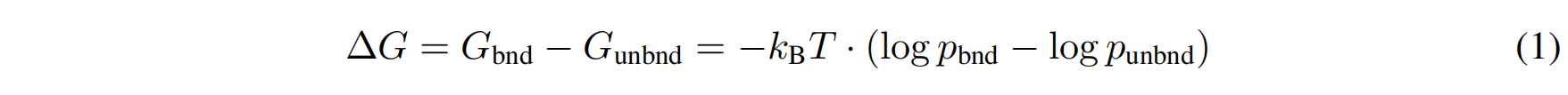
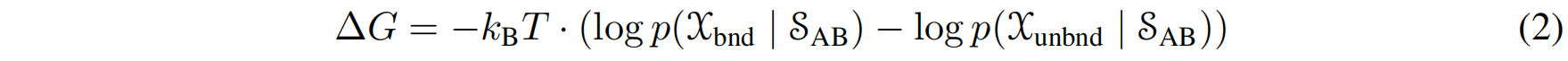
其中,$k_{B}$ 是玻尔兹曼常数,T是热力学温度。这里的 $p_{bnd}$ 和 $p_{unbnd}$ 分别代表给定蛋白质序列 $S_{AB}$ 时,其构象处于结合态( $\mathcal{X}_{bnd}$ )和非结合态( $\mathcal{X}_{unbnd}$ )的条件概率,即 $p(\mathcal{X}_{bnd}|S_{AB})$ 和 $p(\mathcal{X}_{unbnd}|S_{AB})$ 。
直接估算 $p(\mathcal{X}|S)$ 是极其困难的,因为目前的蛋白质结构预测模型难以提供真实的概率解释。为了解决这个棘手的问题,作者巧妙地运用了贝叶斯定理:
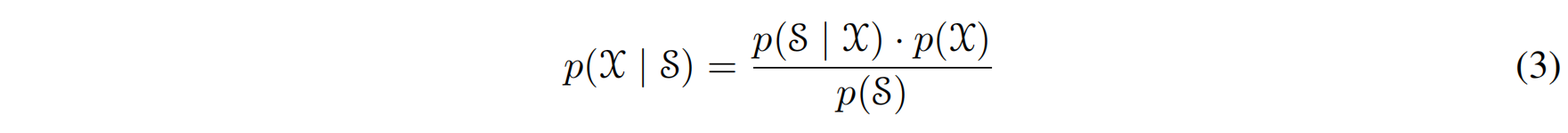
将此式代入 $\Delta G$ 的表达式中,可以消去与序列相关的项p(SAB),从而将 $\Delta G$ 与逆折叠模型可以直接预测的序列条件概率 $p(S|\mathcal{X})$ 联系起来 。
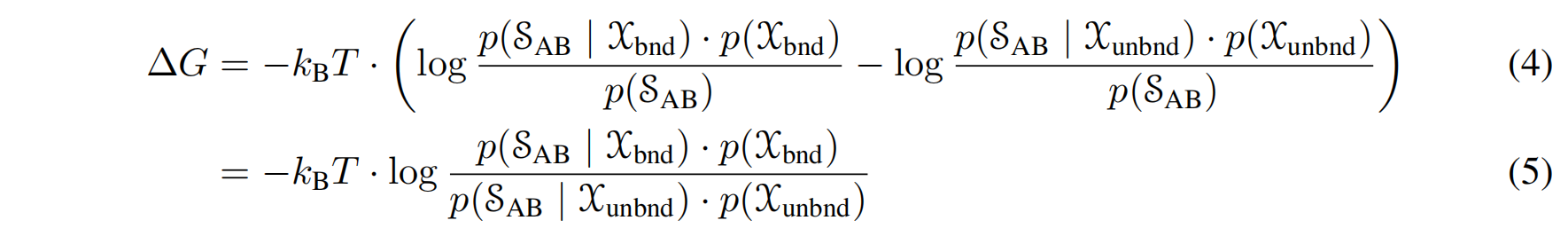
ΔΔG定义为突变体(mut)和野生型(wt)的 $\Delta G$ 之差,即 $\Delta\Delta G = \Delta G^{mut} - \Delta G^{wt}$ 。
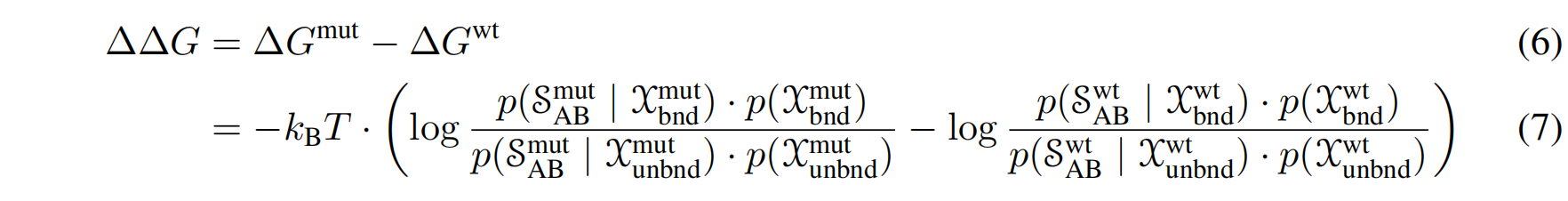
为了进一步简化,作者引入了一个关键假设:蛋白质的骨架结构在突变前后保持不变,即 $\mathcal{X}_{bnd}^{mut} \approx \mathcal{X}_{bnd}^{wt}$ 和 $\mathcal{X}_{unbnd}^{mut} \approx \mathcal{X}_{unbnd}^{wt}$ 。基于此假设,与结构相关的概率项 $p(\mathcal{X})$ 可以被消去,最终得到一个仅依赖于序列似然的 $\Delta\Delta G$ 表达式 :
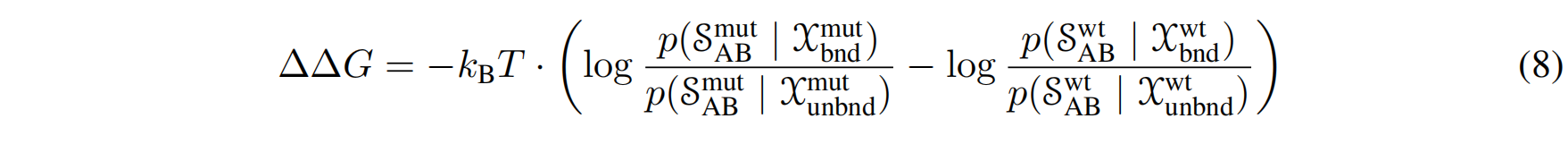
3.2 Probability Estimation
-
结合态 (Bound state) 概率估算:在
$\Delta\Delta G$预测任务中,复合物的结合态骨架结构$\mathcal{X}_{bnd}$通常是已知的。因此,可以直接将复合物的结构和序列输入逆折叠模型,来评估其概率$p_{\theta}(S_{AB}|\mathcal{X}_{bnd})$。 -
非结合态 (Unbound state) 概率估算:非结合态的结构通常没有明确给出 。作者提出了一个合理的近似方法:非结合态可以看作是链A和链B相距很远、相互作用极小的情况 。因此,其概率可以近似为两条链概率的乘积,即分别独立地评估链A和链B的概率,然后相乘 :
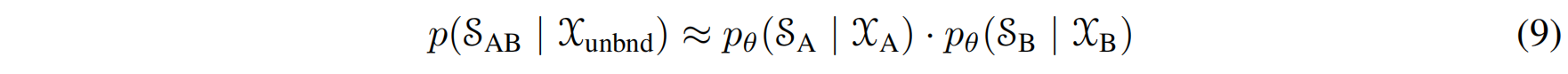
-
无监督方法 BA-Cycle:将上述概率估算方法代入最终的
$\Delta\Delta G$公式,便得到了一个无需训练的(无监督)评估方法,作者将其命名为BA-Cycle 。该方法直接利用预训练好的逆折叠模型(如ProteinMPNN)进行计算 。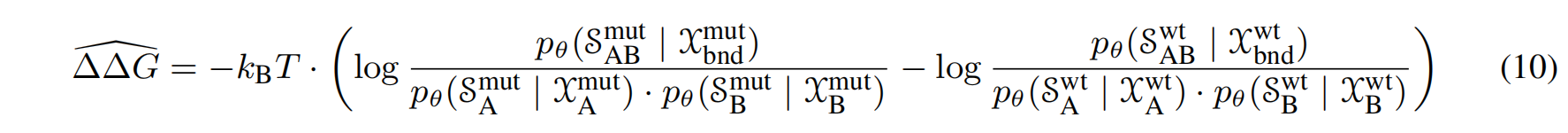
-
与先前工作的比较:作者明确指出,先前的工作在使用逆折叠模型预测
$\Delta\Delta G$时,没有在热力学循环中显式地考虑非结合态$p_{unbnd}$,仅仅比较了结合态的概率差异 。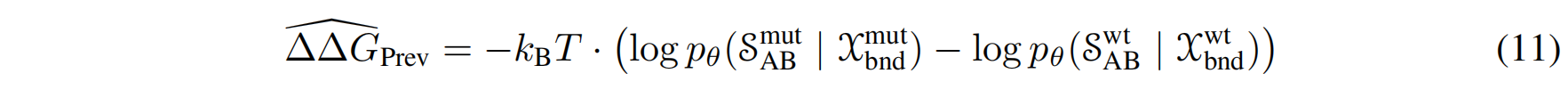
3.3 Supervision
训练目标:BA-DDG的训练目标是最小化预测值与真实 $\Delta\Delta G$ 标签之间的差异,同时要保持从预训练模型中学到的分布知识 。
损失函数:为此,作者设计了一个包含两项的损失函数 $L_{Boltzmann} $:
- 预测误差项:衡量预测值与真实值之间的差距 。
- 分布惩罚项 **:使用KL散度来惩罚微调后的模型
$p_{\theta}$与原始预训练模型$p_{ref}$之间的分布差异 。这一项可以有效防止模型在微调过程中发生“灾难性遗忘”** 。
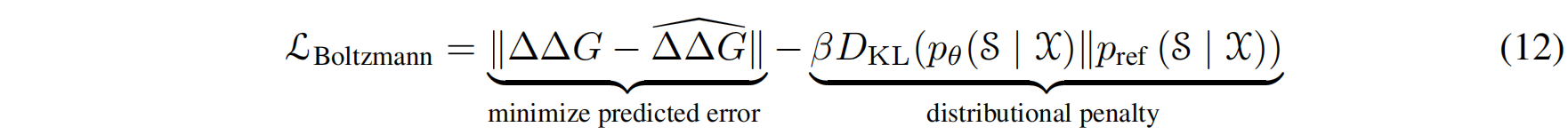
在训练过程中,逆折叠模型的参数$\theta$ 和物理项$k_B T$都被视为可学习的参数进行优化 。
4 Experiments
4.1 Benchmark
- 数据集:实验采用 SKEMPI v2 数据集,这是一个包含了348个蛋白质复合物中7,085个氨基酸突变及其热力学参数变化的权威基准 。为了防止数据泄露,作者采用了按结构划分的3折交叉验证方法,确保每个折叠中的蛋白质复合物都是独一无二的 。
- 评估指标:为了全面评估性能,共使用了7个指标 。
- 5个整体指标:皮尔逊相关系数(Pearson)、斯皮尔曼等级相关系数(Spearman)、最小化均方根误差(RMSE)、最小化平均绝对误差(MAE)以及受试者工作特征曲线下面积(AUROC) 。
- 2个逐结构指标:将突变按其所属的蛋白质结构分组,分别计算每组的皮尔逊和斯皮尔曼相关系数,然后报告这些系数的平均值,这在实际应用中更受关注 。
- 基线模型:作者将他们的方法BA-Cycle(无监督)和BA-DDG(有监督)与当前最先进的各种方法进行了比较 。
- 无监督基线:包括传统的经验能量函数(如Rosetta、FoldX)、基于序列/进化的方法(如ESM-1v、MSA Transformer)以及基于结构信息的预训练方法(如ESM-IF、RDE-Linear) 。
- 有监督基线:包括端到端学习模型(如DDGPred)和在
$\Delta\Delta G$标签上微调过的预训练模型(如RDE-Network、Prompt-DDG、ProMIM) 。
4.2 Main Results
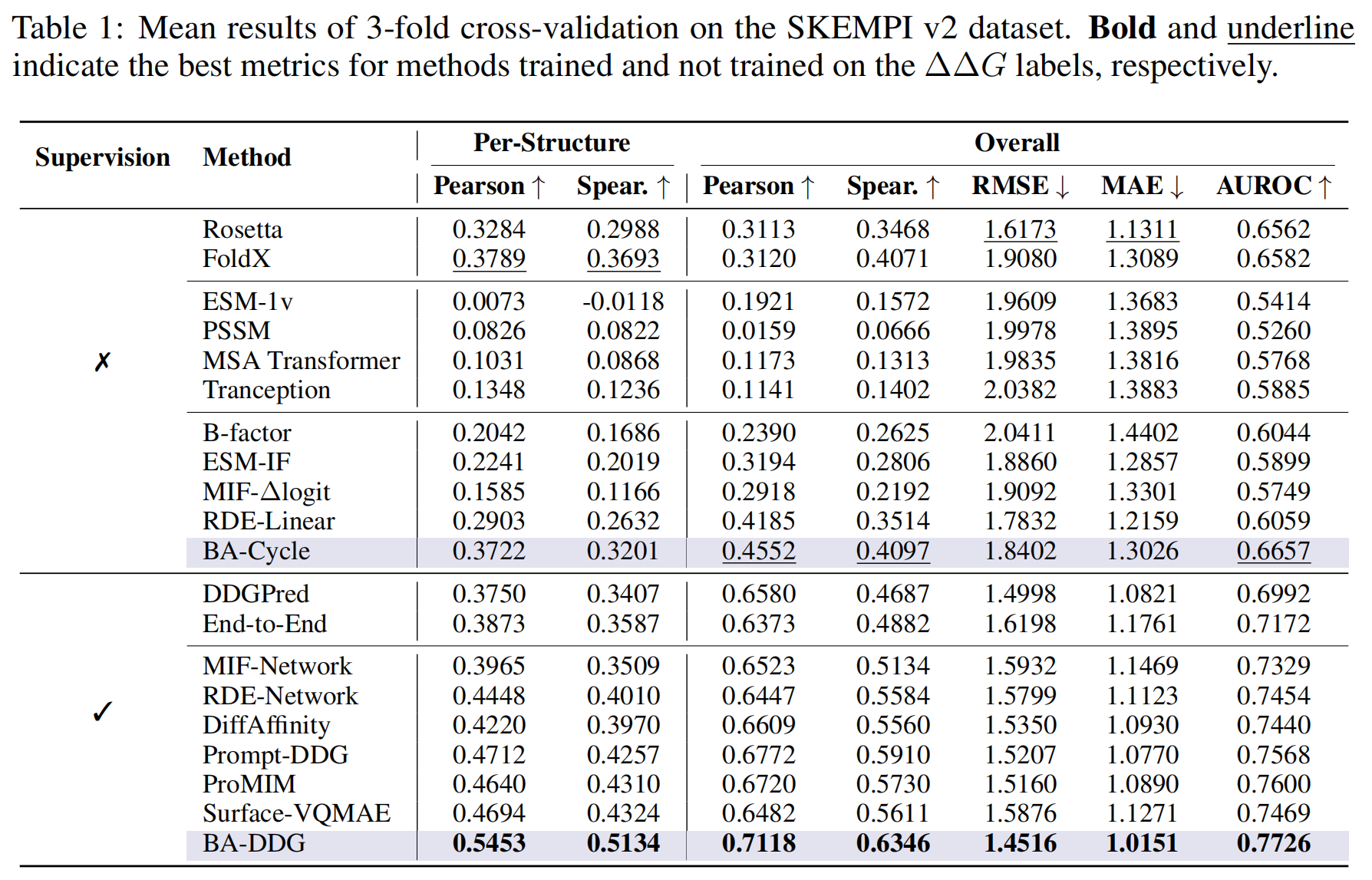
性能对比:如表1所示,BA-DDG在所有评估指标上均优于所有基线模型 。特别是在逐结构(per-structure)相关性上提升显著,表明其在实际应用中更可靠 。无监督版本的
BA-Cycle 性能与传统的经验能量函数相当,并超过了所有其他无监督学习基线 。
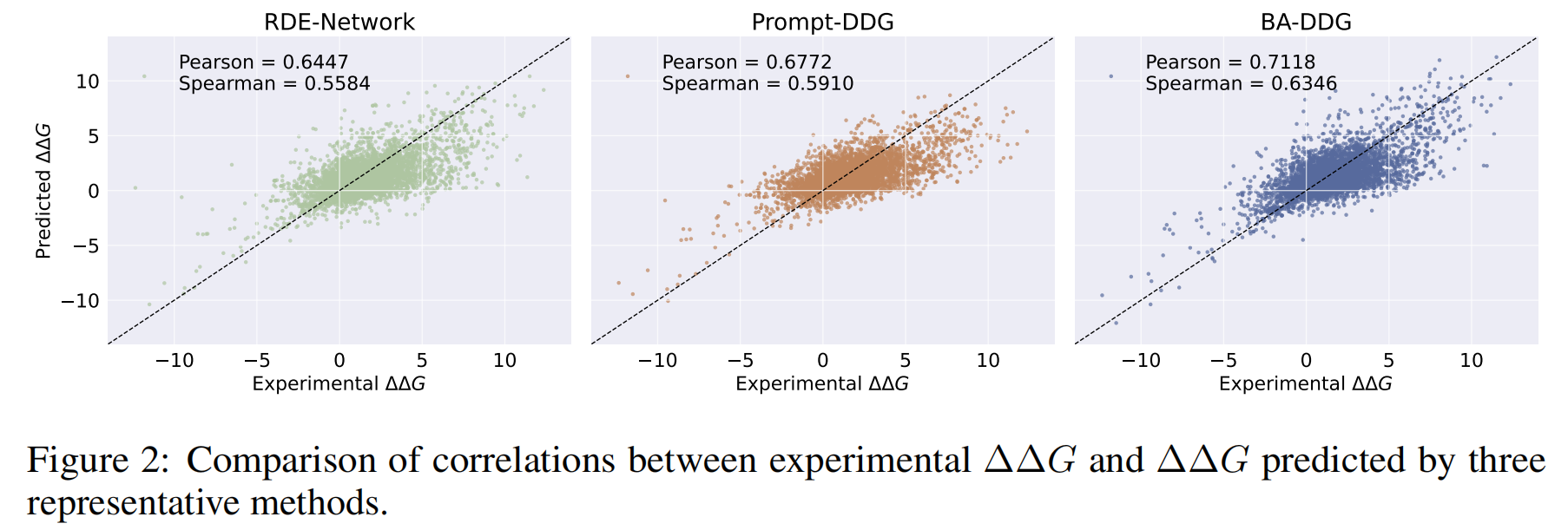
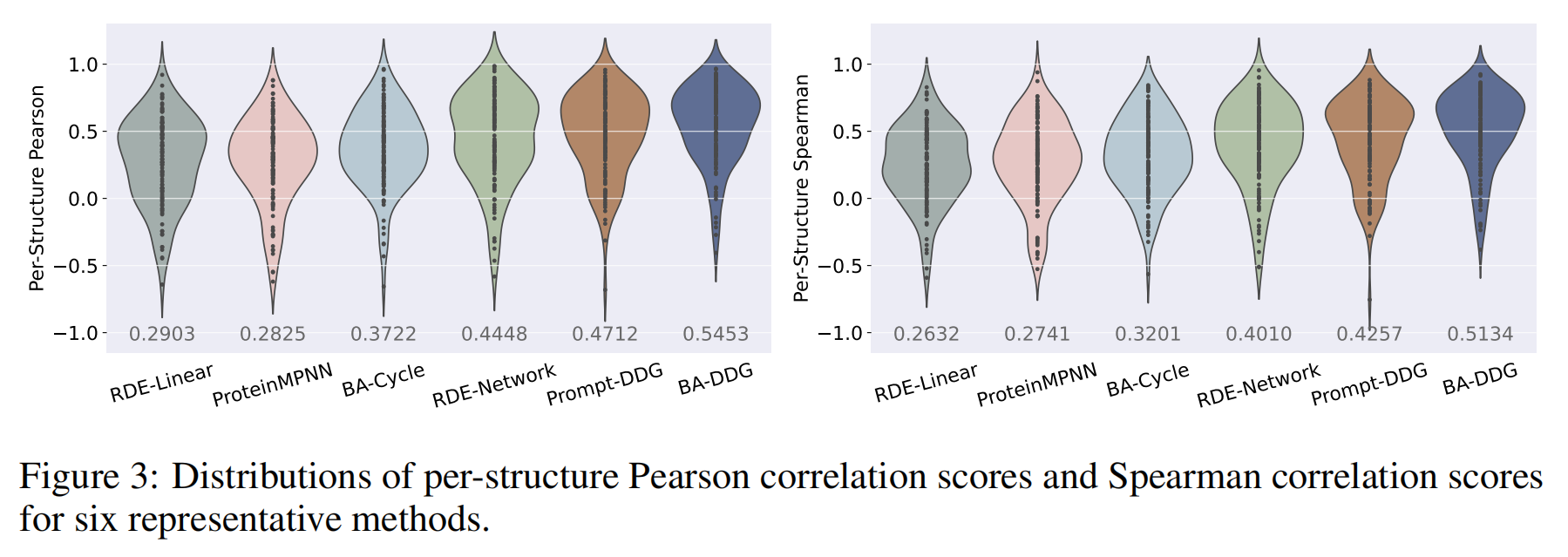
可视化分析:图2的散点图和图3的分布图直观地展示了BA-DDG相较于其他代表性方法(如RDE-Network和Prompt-DDG)具有更好的预测相关性和更优的逐结构性能分布 。
4.3 Ablation Study
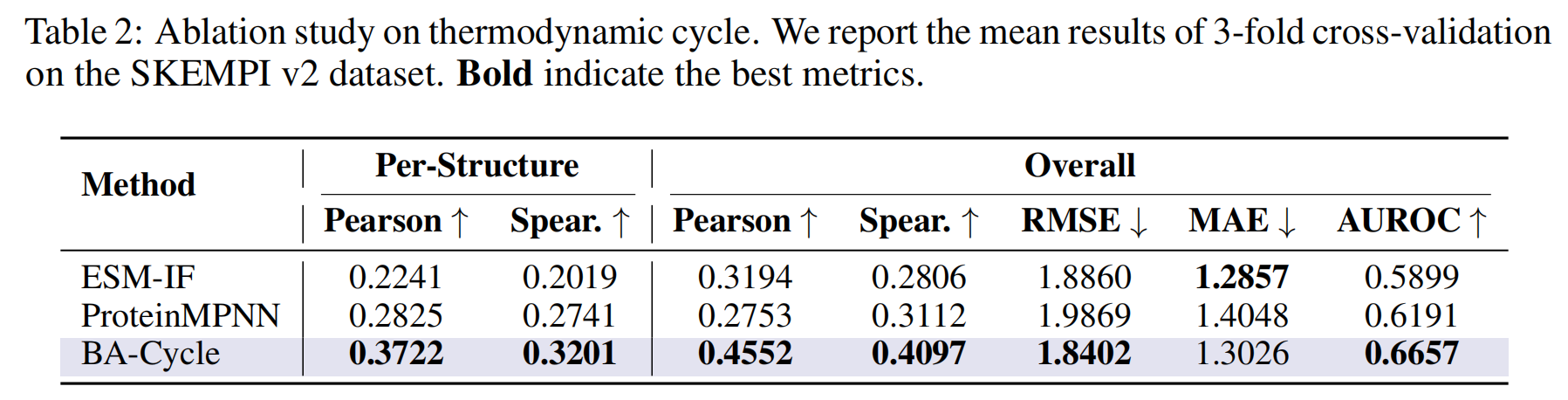
- 热力学循环的有效性:如表2所示,作者比较了他们的无监督方法BA-Cycle与不考虑热力学循环(即忽略非结合态punbnd)的传统逆折叠模型用法(如原始ProteinMPNN) 。结果显示,BA-Cycle的性能显著优于后者,证明了显式地考虑热力学循环对性能至关重要 。
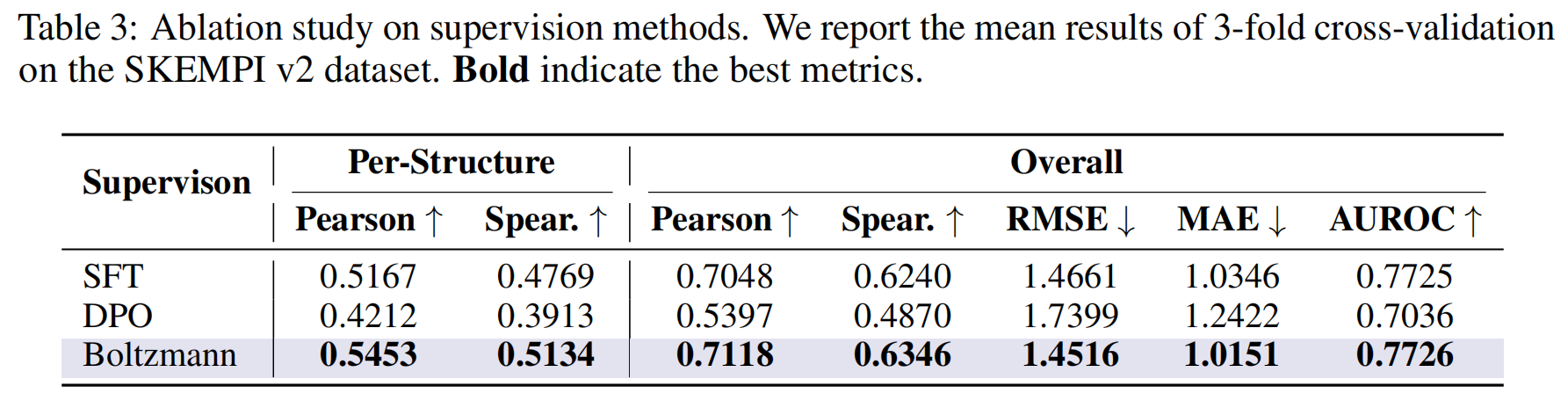
- 监督方法的有效性:如表3所示,作者比较了他们提出的玻尔兹曼监督方法与SFT(监督微调)和DPO(直接偏好优化)等其他对齐技术的性能 。结果表明,玻尔兹曼监督在所有评估指标上均取得了最佳性能,证明了该方法的有效性 。
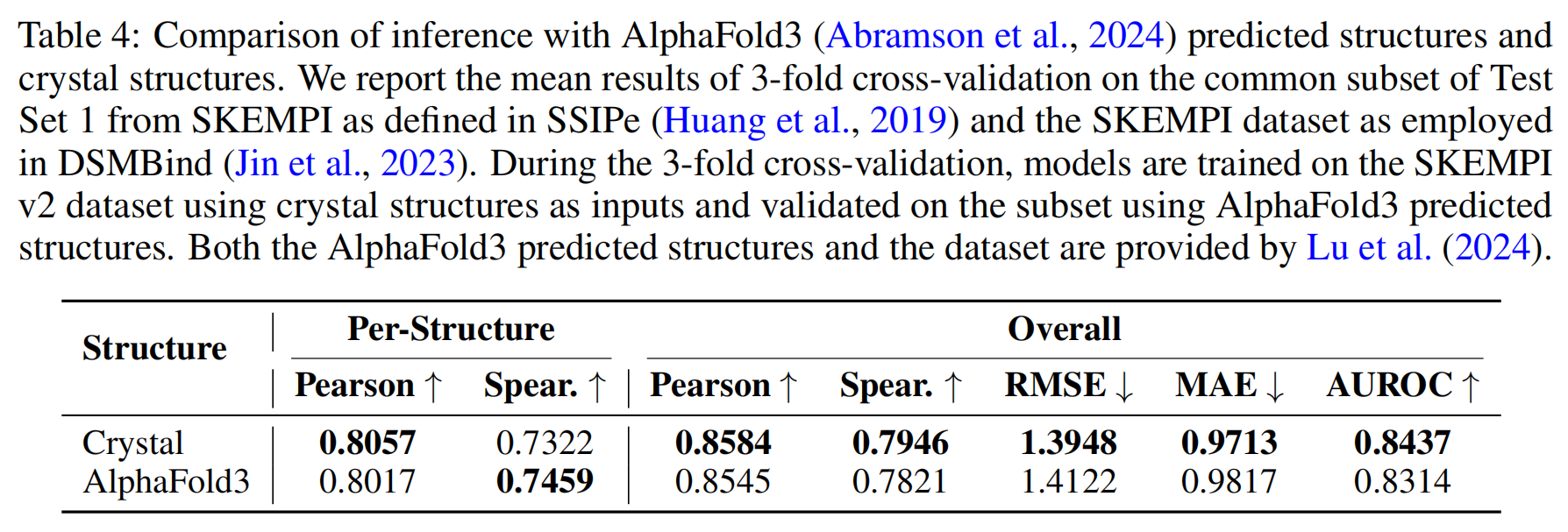
- 使用预测结构进行推理:在实际应用中,往往只有序列信息而没有实验测定的晶体结构 。作者测试了使用AlphaFold3预测的结构作为输入时的模型性能 。如表4所示,尽管使用预测结构的性能略有下降,但差异非常小,这表明该方法并不严格依赖晶体结构,当有合理准确的预测结构时同样有效 。
4.4 Application
4.4.1 Binding Energy Prediction
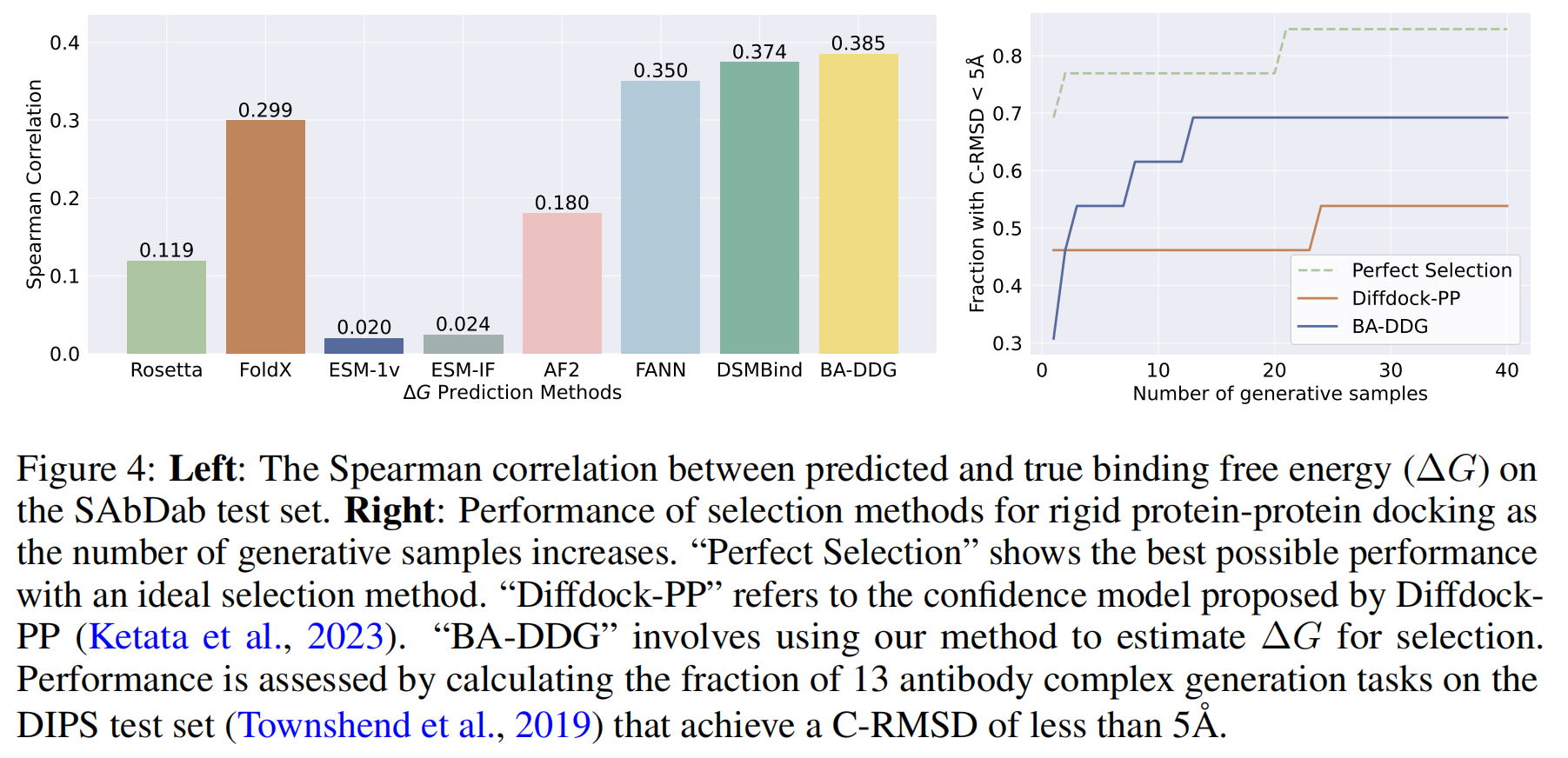
- 背景与方法:抗体设计在治疗癌症和感染等疾病中至关重要 。尽管作者没有为公式(5)中
$p(\mathcal{X}_{bnd})$和$p(\mathcal{X}_{unbnd})$项的抵消提供全面的解释,但BA-DDG可以被用来近似预测绝对结合能($\Delta G$) 。其近似计算公式如下 :
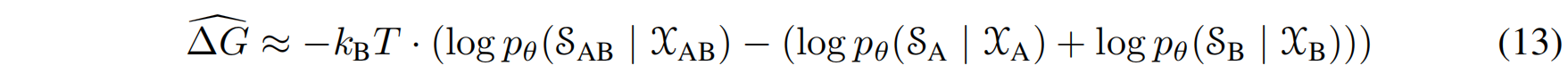
-
实验设置:作者在一个抗体-抗原结合能预测的基准上进行了测试,该实验设置由DSMBind提出 。他们在SAbDab数据集的一个子集上进行了评估,该子集包含566个具有结合能标签的复合物 。
-
结果:如图4(左侧)所示,BA-DDG取得了0.385的斯皮尔曼相关系数,表现优于其他方法 。
4.4.2 Rigid Protein-Protein Docking
- 背景与方法:蛋白质对接的第一步是生成候选的对接构象,第二步则是从这些构象中挑选出最可信的一个作为最终结果 。BA-DDG可以作为一个近似的结合自由能(
$\Delta G$)评估器,并被用作扩散对接过程中的筛选方法 。理论上,一个更低的$\Delta G$值意味着从非结合态到结合态的转变更为有利和自发,因此对应于一个更高置信度的对接构象 。 - 实验设置:作者将BA-DDG集成到DiffDock-PP(一个用于蛋白质对接的扩散生成模型)的流程中,用它来替代原有的置信度模型进行构象筛选 。
- 结果:如图4(右侧)所示,通过将BA-DDG整合到基于扩散的对接流程中,为挑选最 plausible 的对接构象提供了一个稳健的方法 。与DiffDock-PP自带的置信度模型相比,使用BA-DDG进行筛选能够更有效地识别出正确的对接结果(C-RMSD < 5Å) 。
4.4.3 Antibody Optimization
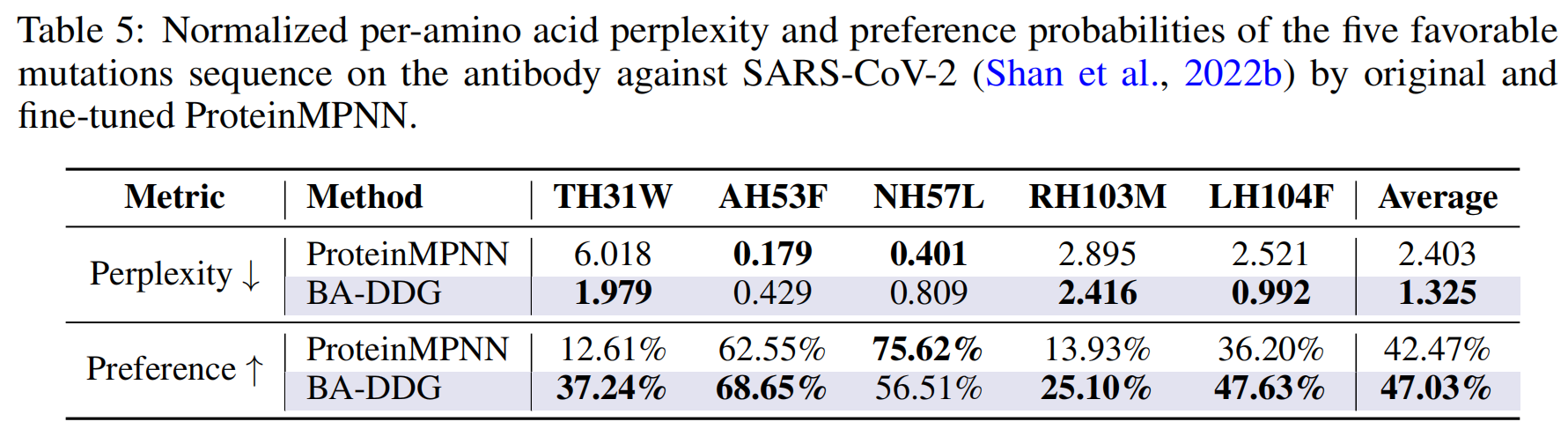
- 背景与方法:除了作为能量评分函数,BA-DDG本身也是一个基于结构的蛋白质设计器,类似于其基础模型ProteinMPNN 。因此,作者好奇经过
$\Delta\Delta G$预测任务微调后的模型是否会倾向于生成亲和力更高的序列 。他们在一个针对SARS-CoV-2的人源抗体优化案例上进行了测试。该案例中,研究人员从494个可能的单点突变中筛选出了5个能显著增强中和效果的突变 。作者使用原始ProteinMPNN和微调后的BA-DDG,计算了这494个突变的困惑度差异(normalized per-amino acid perplexity)和偏好概率(preference probabilities)。 - 结果:如表5所示,对于已知的5个有利突变,微调后的BA-DDG通常给出了比原始ProteinMPNN更低的困惑度和更高的偏好概率 。这一结果表明,为
$\Delta\Delta G$预测任务进行的微调,能够引导模型设计出潜在结合亲和力更高、中和效果更好的抗体序列 。在多点突变上的结果也进一步支持了这一结论 。
