code2vec:pathAttention的代码嵌入表示
Abstract
作者的主要想法是把代码片段用一个固定长度的代码向量来表示。主要是通过主要是把代码通过它的AST解构成一个路径的集合,再同时学习每个路径的表,最后学习怎么样聚合这些信息。
预测函数名方面获得了相对75%的提升
Introduction
目前有很多的向量表示的方法,比如word2vec等等,本文重点放在了code2vec
目标:学习代码的嵌入表示

激励任务:代码片段生成对应的语义标签,具体情况如上图所示,可以看到模型的预测是符合真实的语义信息的,生成的是最有可能的语义标签。
这个方法的难点在于需要学习一个语义标签和整体方法内容的一种对应方式,就需要去聚合上百的表达式、声明等内容把它们融合到一个独立的标签里。
Contribution
文章主要贡献点在于提出了新的网络模型能够进行代码的嵌入表示,可以学习到一个连续的良好的向量
模型的输入是一个代码片段和对应的语义特征,如标签,名字或其他同一类型的文本。假设代码片段为C,对应的标签为L,标签分布可由C的AST路径得到,分布即为 $P(L|C)$

作者还表示模型学习到了像NLP里面的那种语义信息,如上图所示,比如:vector (equals)+vector (toLowerCase)=vector (equalsIgnoreCase)
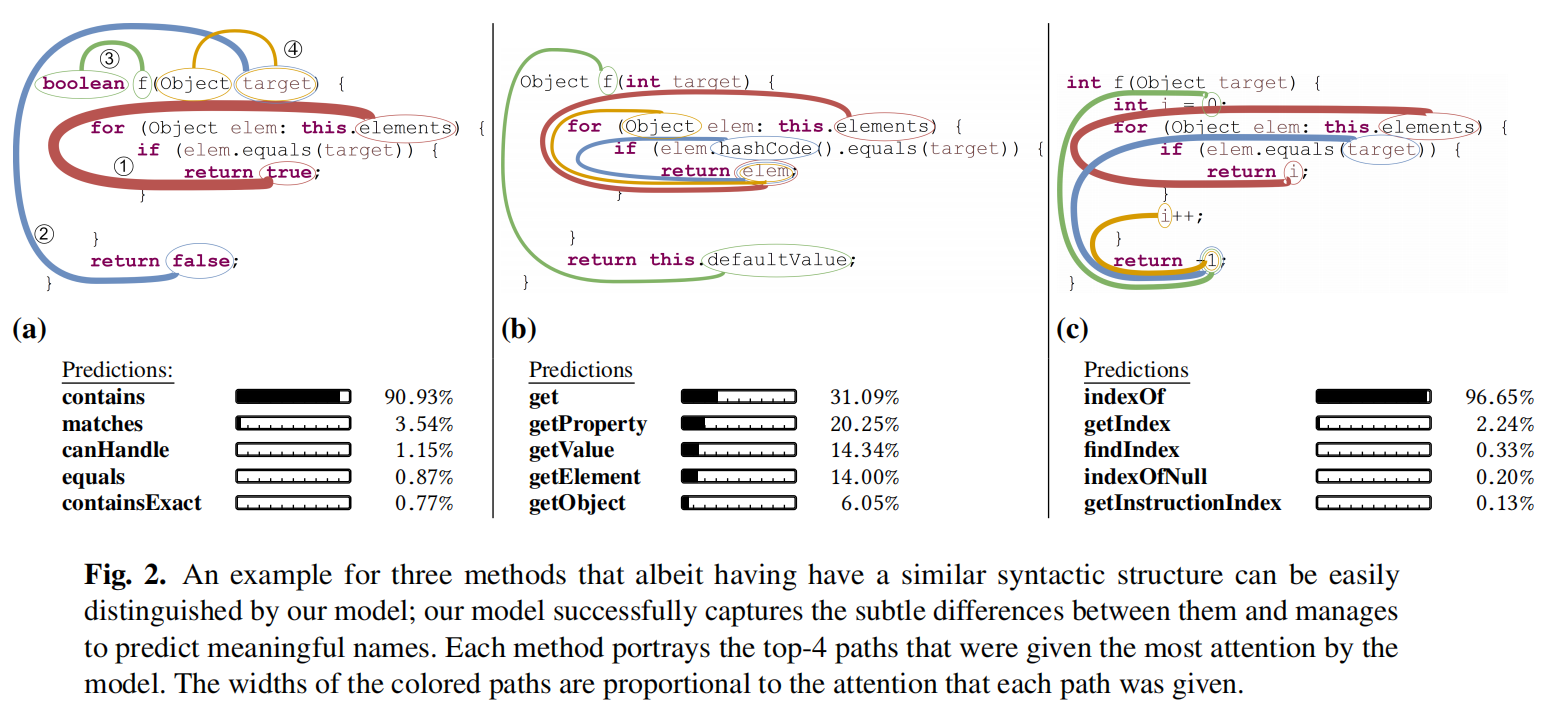
模型同样能识别在结构上很相似但实际语义不同的代码片段,图中4个path是attention权重最高的选出来的
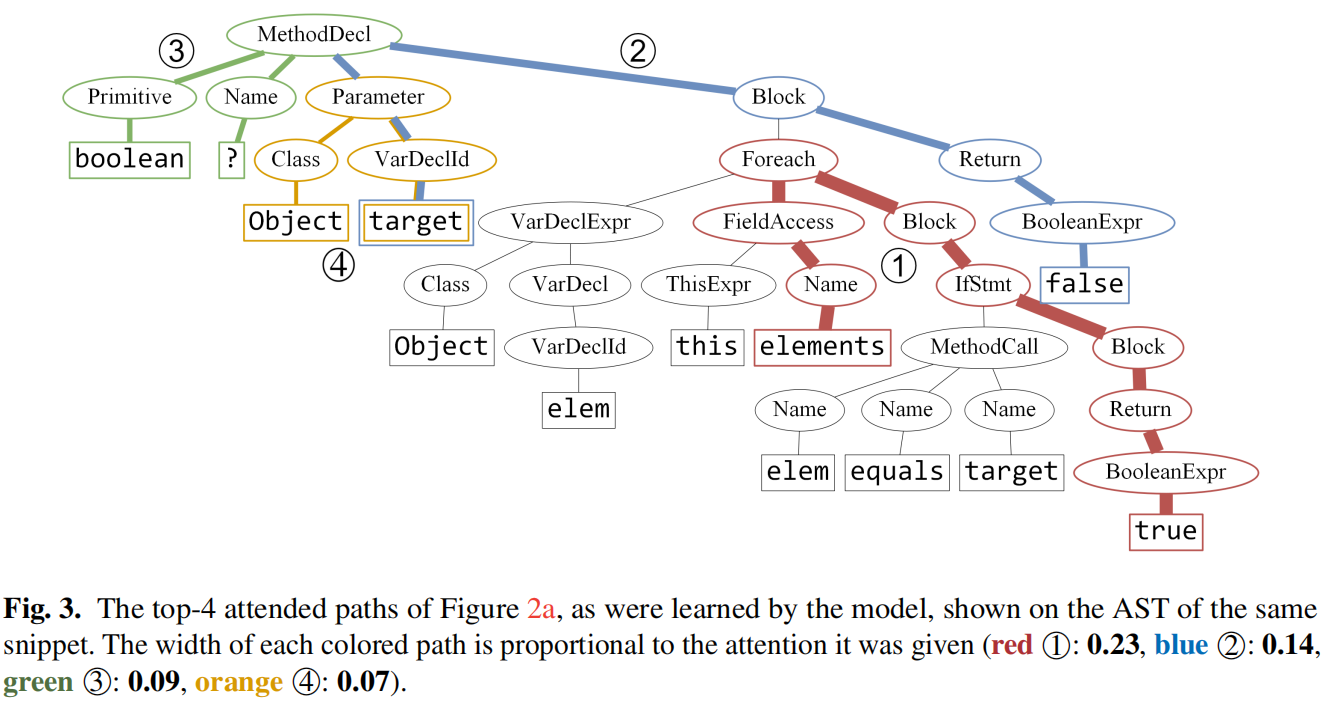
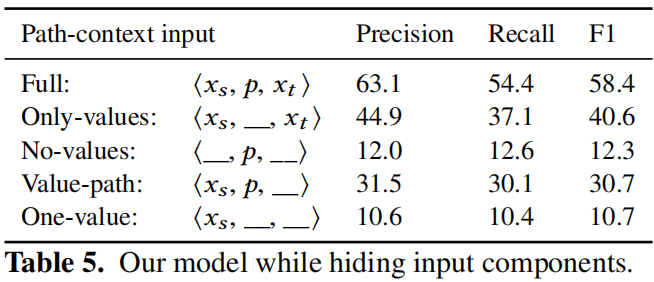
对于代码片段的AST,将每条路径提取出来,路径和结点上的值组成元组称为path-context。结点通过embedding后concat成一个向量来表示path-context,最后通过attention加权融合得到对应方法名的向量
可以发现的是路径长度与attention权重也是成正比的,选择不同的attention方式可能得到不同的路径和结果,同时路径的attention不是常量,在上下文不同的情况下,即使是一模一样的路径得到的attention值也会有不同
关键点:
- 代码片段可以用path-context来高效表示
- 只是一条path-context是不足以做出准确的预测,通过基于注意力的神经网络就能识别出多条路径中更重要的部分,并且聚合它们做出准确的预测
- 微小的不同也能被模型识别出来,即使两个代码片段有着相似的语法结构和大量的相同词汇
- 模型可以用在大语料库,跨项目的方法名预测中
- 尽管该模型是基于神经网络,但是依旧有着较好的可解释性和能发现一些有趣的特性
Model
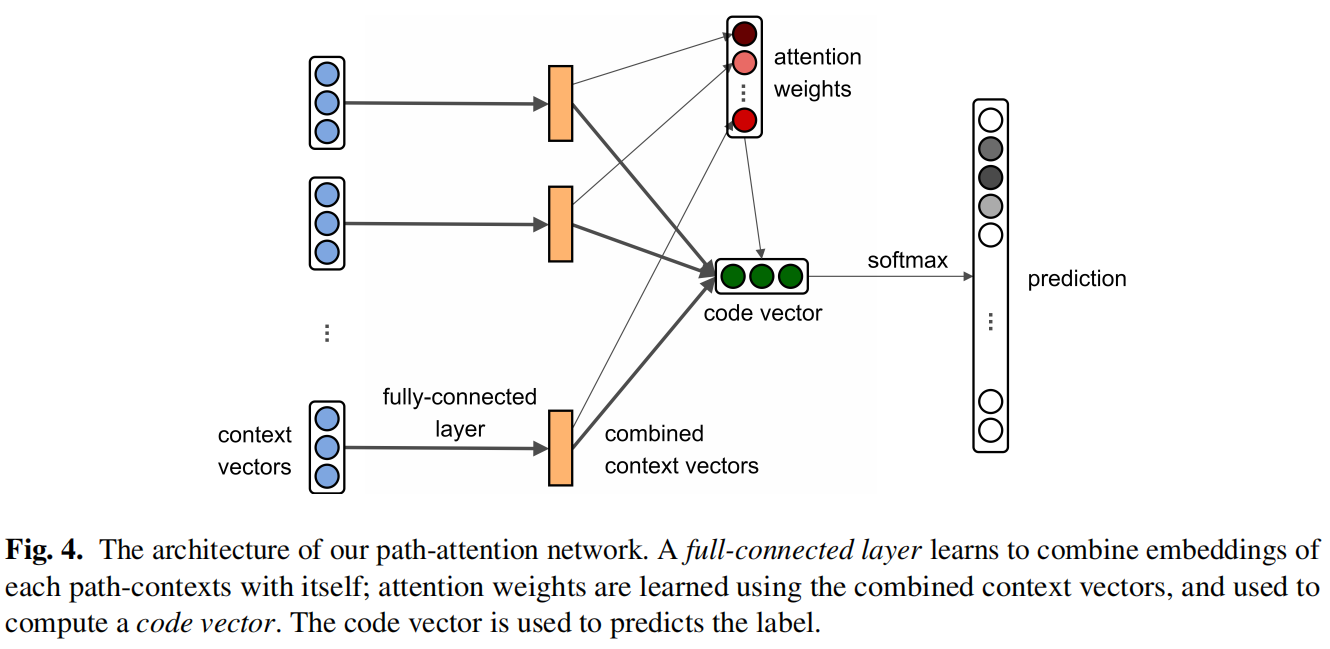
首先对代码片段的每个token和路径做编码
$$
value_vocab\in \mathbb{R}^{|X|\times d}\
path_vocab\in \mathbb{R}^{|P|\times d}
$$
path-context就是将起始token,结尾token和path结合起来
$$
c_i=embedding(<x_s,p_j,x_t>)=[value_vocab_s;path_vocab_j;value_vocab_t]\in \mathbb{R}^{3d}
$$
经过全连接层和激活函数进行特征融合
$$
\tilde{c}_i=tanh(W\cdot c_i)
$$
计算注意力权重,a是全局注意力机制随机初始化的,跟随网络同时进行学习
$$
attention\space weight\space \alpha_i=\frac{\exp(\tilde{c}i^T\cdot a)}{\sum{j=1}^n\exp(\tilde{c}_j^T\cdot a)}
$$
经过加权得到最终表示
$$
code \space vector \space v=\sum_{i=1}^n\alpha_i\cdot\tilde{c_i}
$$
给定一些单词作为候选标签,构成标签矩阵
$$
tags_vocab\in\mathbb{R}^{|Y|\times d}
$$
最终经过softmax计算得到结果
$$
f\space or \space y_i\in Y:q(y_i)=\frac{\exp(v^T\cdot tags_vocab_i)}{\sum_{y_j\in Y}\exp(v^T\cdot tags_vocab_j)}
$$
Experiment