GRACE:节点级无监督图对比学习
Abtract
作者提出了一个节点级的无监督表示对比学习框架,通过corruption生成两个视图,通过最大化两个视图结点表示的一致性来学习结点的表示
提出了一种在结构和属性层面上生成图视图的混和方案
实验表示尽管这种方法简单,但是还是大大的优于了目前的SOTA方法,以及在transductive和inductive学习任务进行了实验
Introduction
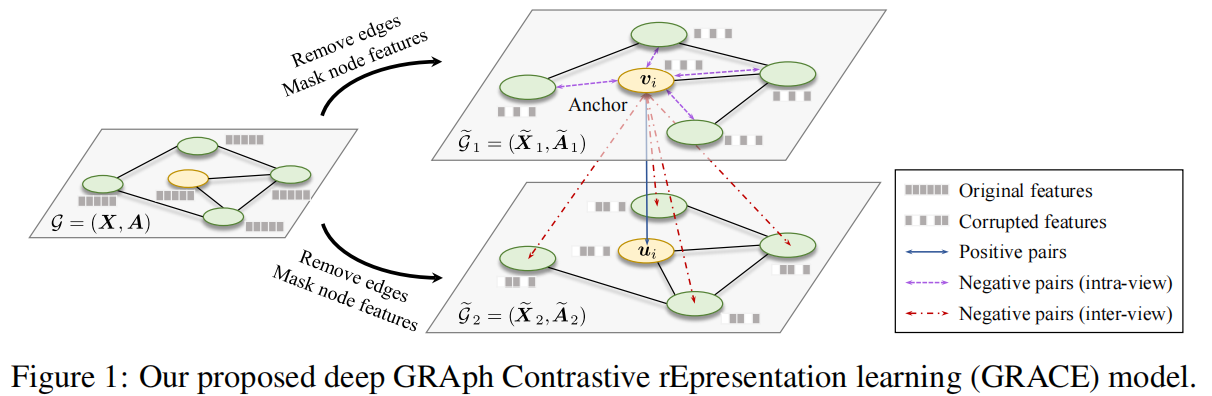
本文受激励于DGI(Deep Graph InfoMax),它提出了一种在图领域的基于互信息(MI:Mutal Information)最大化的目标
- 先是部署了一个GNN去学习结点的嵌入表征(node embedding),然后获得一个全局的总结嵌入表征(graph embedding)
- 目标是区分原始图中的节点和损坏图中的节点来最大化节点嵌入和图嵌入之间的MI
- 缺点:
- DGI使用 mean-pooling readout 函数,不能保证图嵌入可以从节点中提取有用的信息,因为它不足以从节点级嵌入中保存独特的特征
- DGI使用特征变换来生成损坏视图。然而,该方案在生成负节点样本时,在粗粒度级别考虑损坏节点特征。当特征矩阵稀疏时,只执行特征变换不足以为损坏图中的节点生成不同的邻域(即上下文),导致对比目标的学习困难
本文提出了一个简单但有效的无监督图对比学习的框架,不是通过结点和全局的对比,而是关注于节点级的对比
- 先是通过随机的corrpution操作来生成两个相关的图视图,然后最大化一致性
- 考虑拓扑和节点属性级别的损坏,即去除边和mask特征
Model
Perliminaries
$\mathcal{G}=(\mathcal{V},\mathcal{E}),\mathcal{V}={v_1,v_2,\cdots,v_N},\mathcal{E}\subseteq\mathcal{V}\times\mathcal{V}$
特征矩阵:$X\in \mathbb{R}^{N\times F}$,其中 $x_i\in \mathbb{R}^F$
邻接矩阵:$A\in {0,1}^{N\times N}$,当 $(v_i,v_j)\in \mathcal{E}$ 时,$A_{ij}=1$
在训练过程中没有给 $\mathcal{G}$ 的结点类别信息,目标是学习一个GNN的编码器 $f(X, A)\in \mathbb{R}^{N\times F’}$,输入的是图的结构和特征,输出是节点的低维度表示
将 $H=f(X,A)$ 作为学习到的表示,$h_i$ 是结点 $v_i$ 的嵌入表示
Contrastive Learning of Node Representations
每次迭代生成两个视图,分别是 $G_1,G_2$ ,生成视图结点的嵌入表示 $U=f(X_,A_)$
两个视图中同一结点为正样本,其他结点为负样本,即有M个结点,负样本就是2M-2个
Graph View Generation
两种操作:
- RE(Removing edges)
- 随机删除一些边
- 采样一个随机mask矩阵,如果原始图中 $A_{ij}=1$,则它的值来自伯努利分布 $R_{ij}\sim \mathcal{B}(1-p_r)$,否则 $R_{ij}=0$,最终的邻接矩阵可以计算为 $\tilde{A}=A\circ R$
- MF(Masking node features)
- 在结点特征用0随机屏蔽部分维度
- 对随机向量 $m\in {0,1}^F$ 进行采样,每个维度都独立的从概率为 $1-p_m$ 的伯努利分布中提取,生成的结点特征计算为 $\tilde{X}=[x_1\circ m;x_2\circ m;\cdots,x_N\circ m]^T$
RE和MF方案在技术上与Dropout和DropEdge相似
实验表明,我们的模型在温和的条件下对 $p_r$ 和 $p_m$ 的选择不敏感,因此原始图没有被过度损坏
Experiment