论文地址:Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks
论文实现:https://github.com/cbfinn/maml
博客地址:http://bair.berkeley.edu/blog/2017/07/18/learning-to-learn/
MAML:元学习模型无关的快速适应神经网络
Abstract
与任何只要是梯度下降训练的模型都是相兼容的,能够适应不同问题的模型无关的元学习方法,主要目标是训练不同的任务,解决新任务下只有很少的数据的问题,最终训练出来的模型能够方便的微调
Introduction
作者提出了泛化的模型无关的元学习算法,主要关注于深度神经网络模型,关键思路是训练一个模型初始化参数使得模型遇到新任务时,经过少量的梯度更新就能够最大化性能,产生不错的结果。学习过程可以被视为最大化新任务的损失函数相对于参数的敏感性
Model-Agnostic Meta-Learning
Meta-Learning Problem Set-Up
few-shot 元学习的目标是训练一个模型,只使用少量数据点和训练迭代即可快速适应新任务。我们考虑一个模型,表示为f,它将观测值x映射到输出a,在元学习过程中,该模型被训练成能够适应大量或无限数量的任务。每个任务 $T={L(x_1,a_1,…,x_H,a_H),q(x_1),q(x_{t+1}|x_t,a_t),H}$ 由损失函数L,初始观测值分布 $q(x_1)$ 和分布变化过程 $q(x_{t+1}|x_t,a_t)$ 与训练周期H组成
在元学习场景中,对所有任务考虑一个任务分布 $p(T)$ ,从 $p(T)$ 抽取一个新任务,给k个样本去训练并得到相应的loss,然后在新的样本上测试。最后在 $p(T)$ 中抽样新任务来测试性能
A Model-Agnostic Meta-Learning Algorithm
过去的方法要用到所有的数据集或是在测试时与非参数方法相结合,作者提出这个方法的直觉来源于一部分内在参数是可以迁移的
对于一个参数模型 $f_\theta$ 有参数为 $\theta$,在一个新任务 $T_i$ 上适应的时候参数 $\theta$ 变成 $\theta_i’$
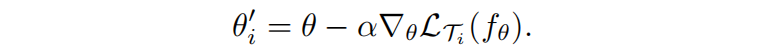
模型参数是通过优化 $f_{\theta’}$ 在从 $p(T)$ 采样的任务对于 $\theta$ 的性能来训练的,平均意义上的对所有任务的局部最优
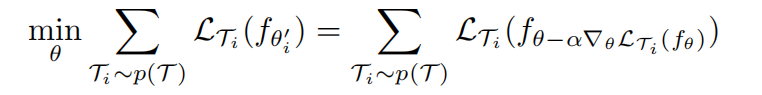
通过随机梯度下降(SGD)进行跨任务的元优化,使模型参数 $\theta$ 更新如下
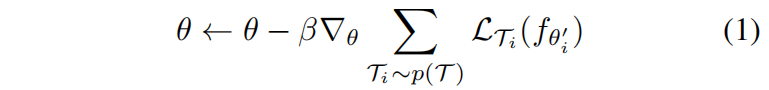
具体的算法如下

外层循环更新 $\theta$ ,内层循环对每个任务更新得到微调之后的 $\theta_i’$
可以看到在外层循环更新 $\theta$ 的时候没有对 $\theta$ 做梯度,而是间接的通过 $\theta_i’$ 来评估,意思其实是本身 $\theta$ 的性能我们并不关心,我们关心的是 $\theta$ 经过调整后做得好不好
Experiment
三个主要问题:
- MAML真的能够在新任务上快速学习吗
- MAML真的可以把元学习用到不同领域,包括有监督的回归,分类,强化学习吗
- 通过MAML学到的模型真的能够通过额外的梯度更新继续提升吗
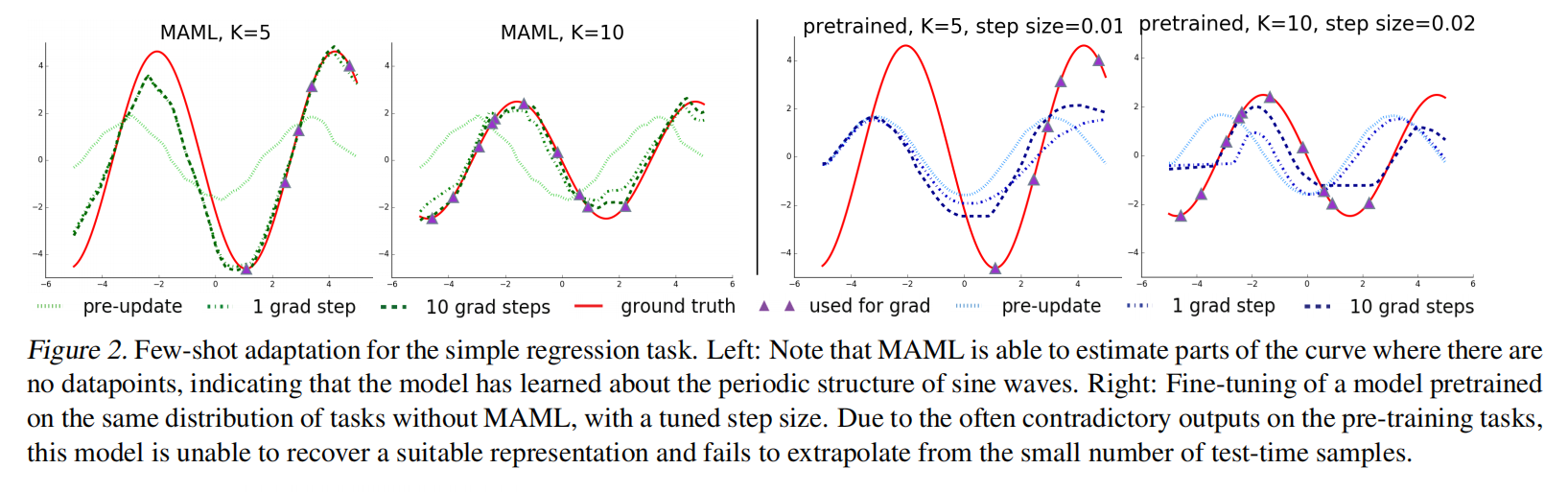
可以看到在MAML中更新10次梯度基本上抓取到了真实情况了,然而预训练模型却很难学习到这种情况。因为类似于MAML是个教练,只要求教出来的学生效果好,本身效果好不好不重要;但是预训练模型要求本身好,但是自己调几步之后不见得好,因为原本已经是可以说是最好的了


