论文地址:AST-trans:code summarization with efficient tree-structured attention
AST-trans:父子和兄弟结点做树注意力
Abstract
AST包含了结构信息但是比对应的原代码长很多,目前方法忽略了长度限制简单粗暴的把整个AST丢进编码器,这种方法难以有效利用关系依赖而且引起巨大的计算开销。本文提出AST-trans利用两种结点关系,祖先后代和兄弟关系,使用树结构注意力对相关和不想关结点分配权重,进一步提出了一个有效的实现来支持快速并行计算的树结构注意
Introduction
线性化的AST比对应的原代码长很多,一些线性算法甚至增加长度,比如线性化SBT使得扩大了数倍,这使得模型很难准确探测出有用的依赖关系。此外也带来了巨大的计算负担,比如基于transformer的SOTA方法的注意力操作随着序列长度增加也在增加
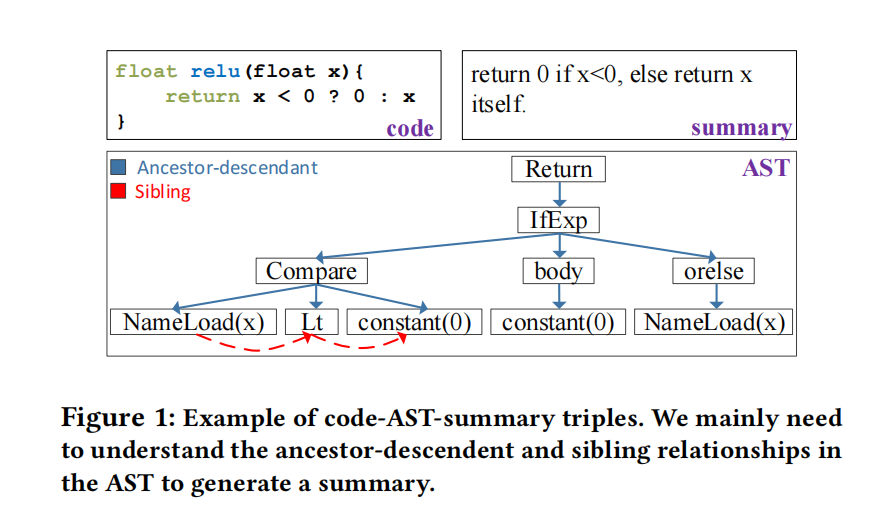
本文假设AST结点状态最受两点影响:1. 祖先-后代结点,表达了不同层次的跨block关系;2. 兄弟结点,表达了一个block内的时间关系。需要祖先-后代结点来理解高层次语义,兄弟关系理解低层次语义,这俩已经够生成注释和建模整个结点需要的注意力
主要贡献:
- AST-trans线性复杂度比标准的transformer二次复杂度编码长AST更高效
- 利用理论和经验证据,对不同实现的计算复杂度进行了全面的分析
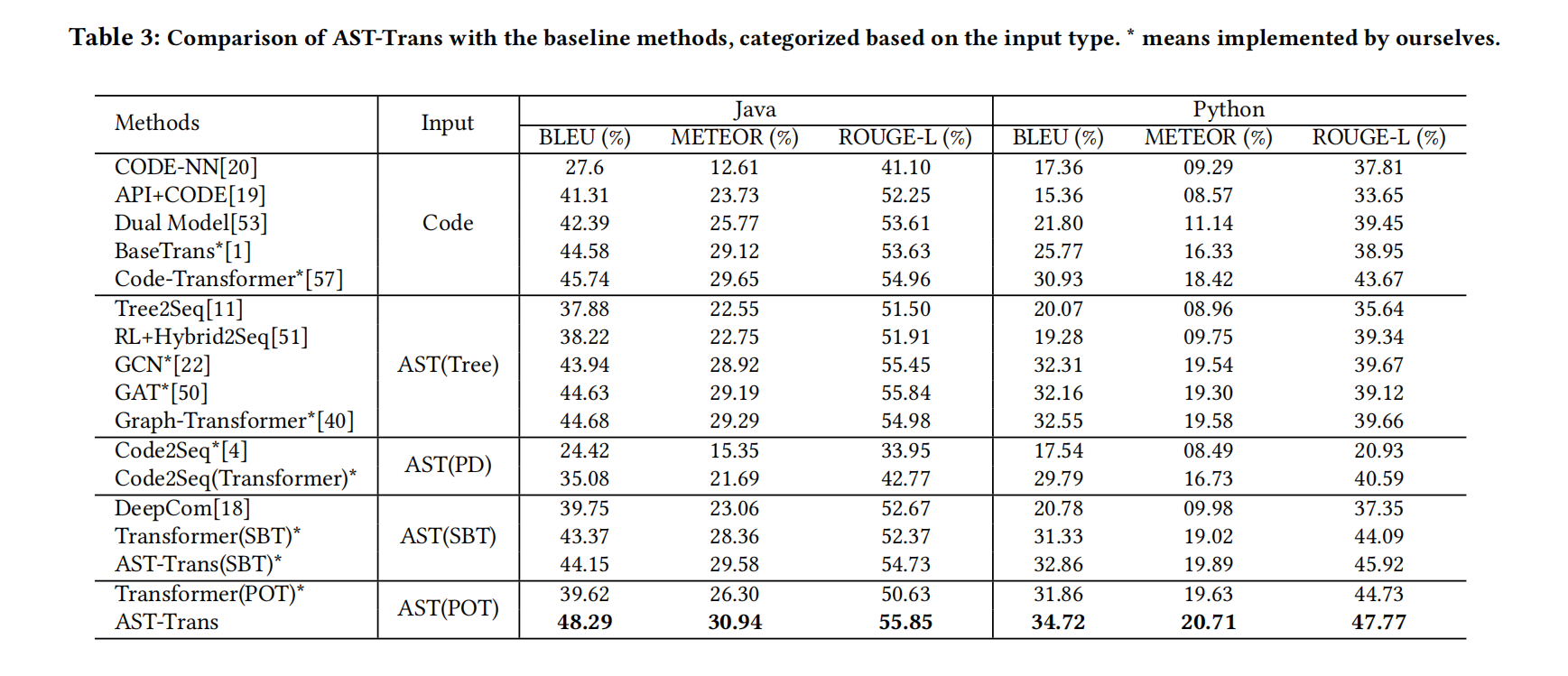
- 在Java和python数据集上显示了AST-trans能达到SOTA
- 比较了AST编码的代表性方法,并讨论了它们的优缺点
AST-TRANS
AST Linearization

先序遍历(POT),基于结构遍历(SBT),路径分解(PD)
Relationship Matrices
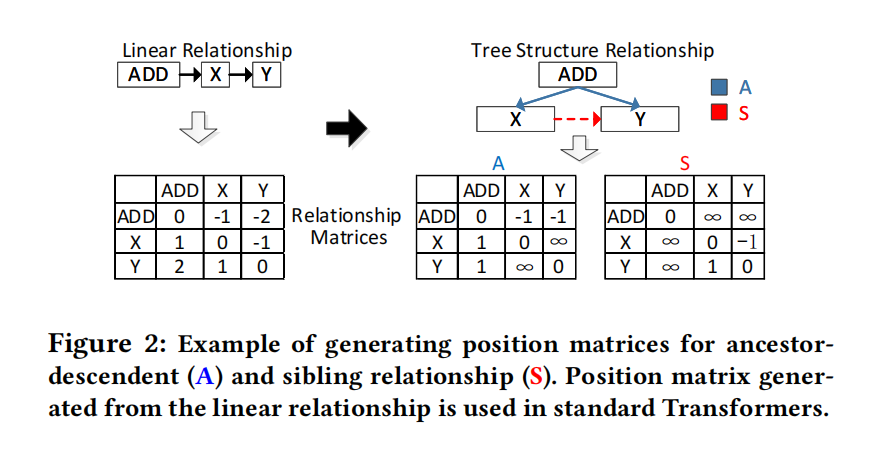
祖先-后代用A矩阵表示,兄弟关系用S矩阵表示,A矩阵的值是计算的最短路径距离,S矩阵的值是AST中水平兄弟距离,P是相对距离门槛
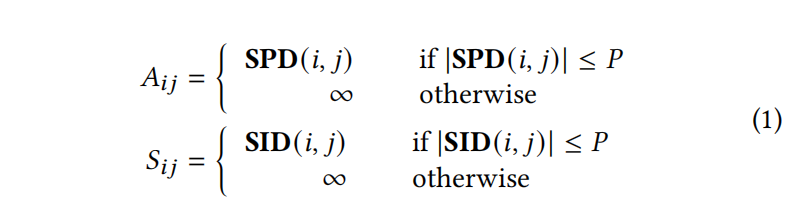
Tree-Structured Attention
Self-Attention
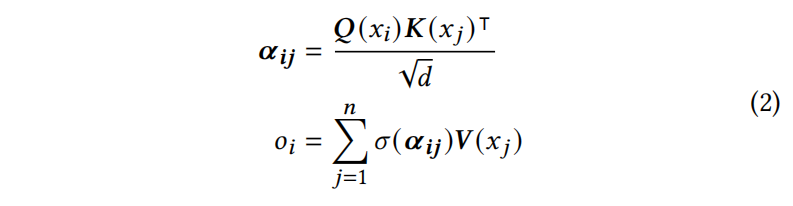
Relative position embedding
公式2没有位置信息,初始的transformer用的绝对位置嵌入,本文这里用相对位置编码(在代码摘要任务更有效),相对位置 $\delta(i,j)$ 反映了 $n_i$ 和 $n_j$ 之间的成对距离
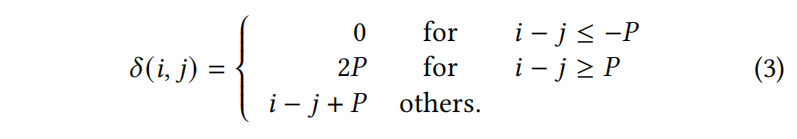
Disentangled Attention
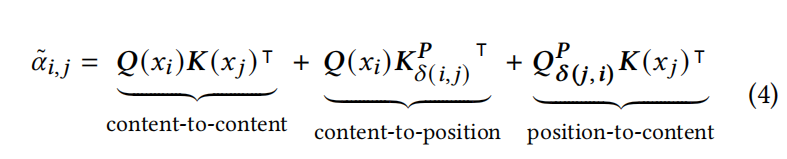
Attention with Tree-Structured Relationships
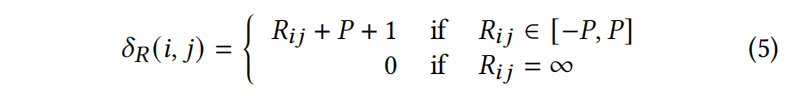
我们的方法本质上用 $\delta_R(i,j)$ 代替了线性关系下定义的相对距离,其中𝑅代表树结构中的祖先-后代关系𝐴或兄弟关系𝑆
这里有两种关系,每种关系对应一个头,这样在顶层的transformer上就不会增加额外参数
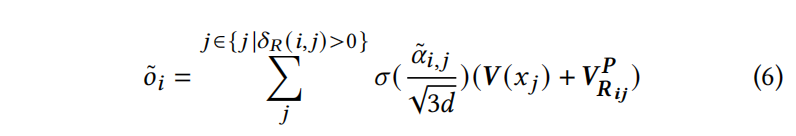
$V^P$ 表示相对距离的值投影矩阵,$V^P_{R_{ij}}$是 $V^P$ 的第𝑅𝑖𝑗行。这里可以看到计算出来的 $\delta_R(i,j)$ 是大于0的,是为了减少了自注意力时的时间和空间复杂性
Efficient Implementation
标准的transformer随序列增加开销增加,AST-Trans可以通过只计算 $\delta_R(i,j)>0$ 的部分来减轻开销,类似于滑动窗口的想法将注意力计算限制在一个固定距离
通过滑动窗口,可以将序列数据中的节点对规划成线性分布(通过忽略 $\delta(i,j)=0$ 或 2P−1 的节点对),并与矩阵划分并行计算。但是这种技术并不适用,因为相关节点的位置分布随着每个树状结构的变化而变化
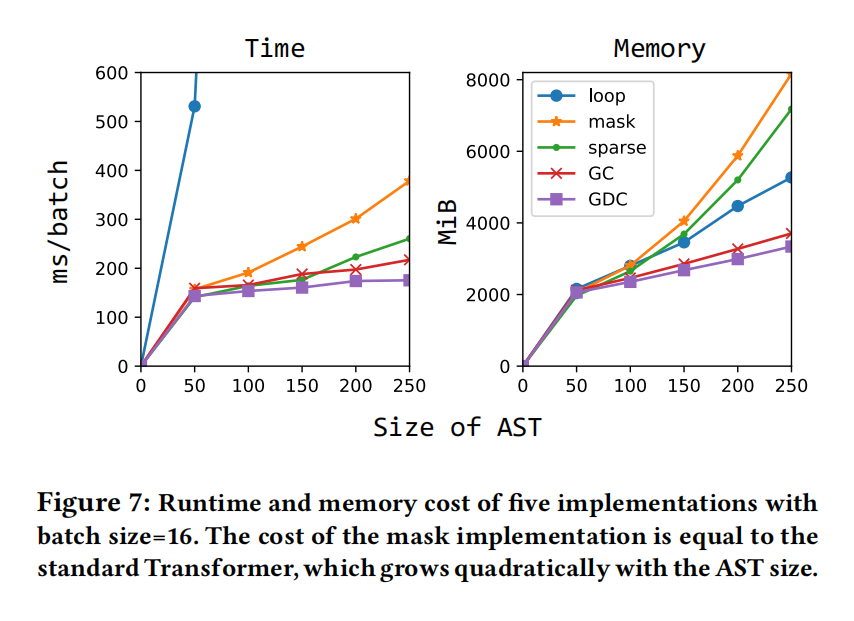
介绍以下5个AST-Trans的备选实现,并讨论其优缺点:
Mask
在计算所有节点之间的全部注意力后,屏蔽 $\delta_R(i,j)=0$ 的注意力得分,它具有与标准transformer相同的二次时间和空间复杂度
Loop
循环 $\delta_R(i,j)>0$ 的节点对 ,并计算注意力分数,有效率但不支持并行处理
Sparse
把 $\delta_R$ 存储为稀疏矩阵 $ST(\delta_R)$ ,用pytorch这样的框架会自动跳过0元素。对于content-to-position和position-to-content可以用,对content-to-content就用不了,还是得用mask或loop方法
Gather with COO (GC)
基于Sparse的方法,content-to-content方法可以通过额外的聚集操作优化。GC的核心思想是将需要计算出来的查询-键对放成一对一的对应关系,并将它们存储为密集的矩阵
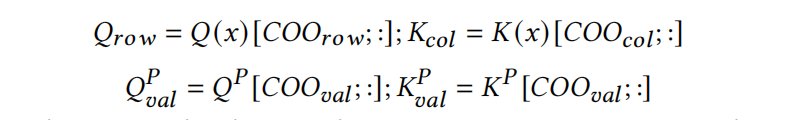
计算中所进行的聚集操作总数是 $\delta_R$ 中非零元素的4倍;2倍用于聚集内容,2倍用于聚集位置
Gather with decomposed COO (GDC)
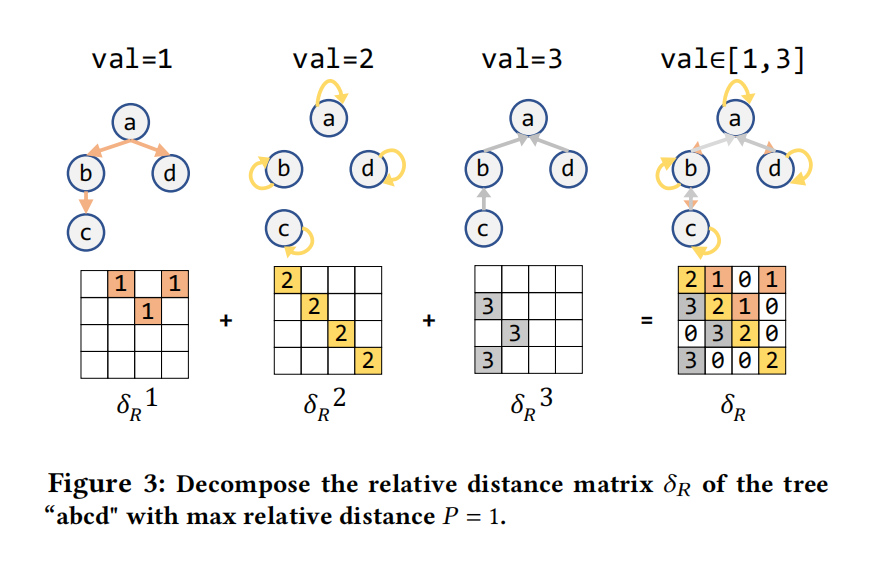
为了减少GC中的聚集操作,使用了矩阵分解操作,把原本的 $\delta_R$ 对应的矩阵分解为三个子矩阵,然后聚集content的嵌入如下
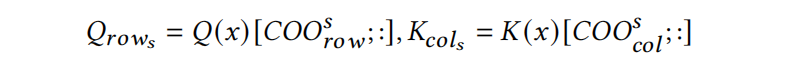
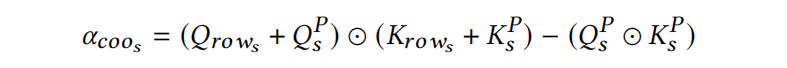
最后把所有的 $\alpha_{coo}$ 加起来
这样做有三个好处:
- $K^P$ 和 $Q^P$ 可以被重用,因为每个 $Q_{row_s}$ 和 $K_{row_s}$ 都有相同的相对距离s,s的位置嵌入可以直接添加到content中,而无需聚集操作
- 只需要四分之一的聚集操作
- 只需要一次点积,后面那次点积可以重用
Complexity Analysis
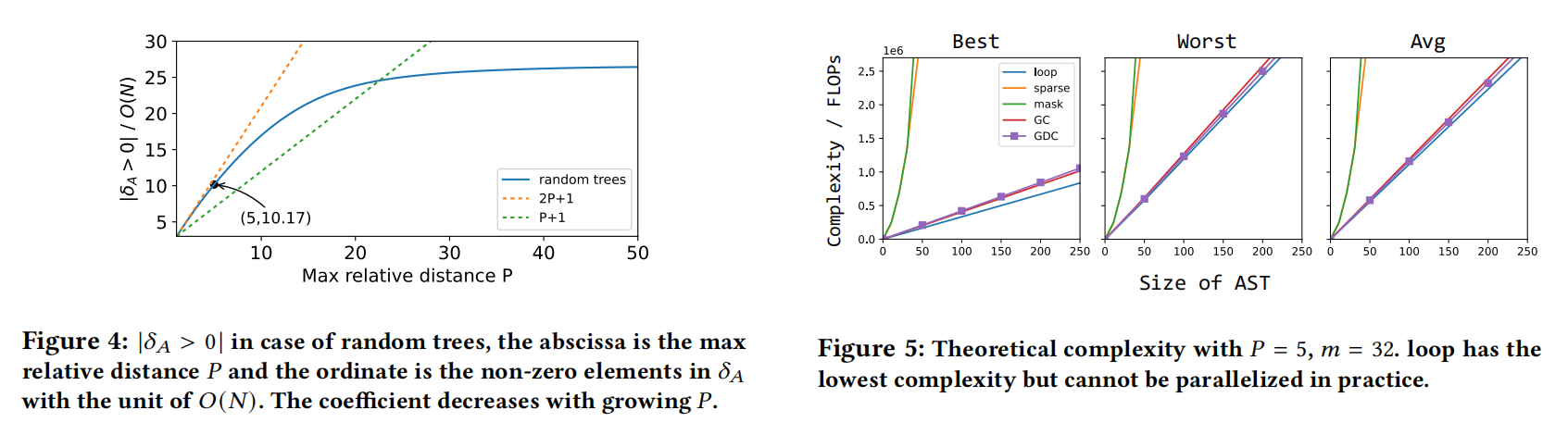
这一节主要讨论上述五种方法最好,最差和平均的复杂度
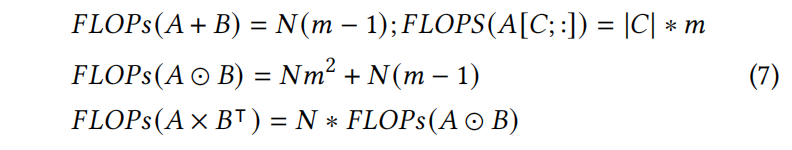
A和B是[N, m]矩阵,A[C; :]表示用C作为索引聚集A,|C|是C的元素个数
具体的计算复杂度看原文,比较硬核
Experiment