论文地址:Improved Semantic Representations From Tree-Structured Long Short-Term Memory Networks
Tree-LSTM:把LSTM推广到树结构
Abstract
自然语言也有句法特征,可以把单词和短语结合起来,因此提出了Tree-LSTM
Introduction
大多数短语或句子的分布式表示分为三类:bag-of-words模型、sequence模型、tree-structured模型。词袋模型直接使用词汇的统计信息,没有考虑词汇的顺序,序列模型考虑的是序列结构,树型结构模型通过在给定句子的语法结构树上进行获取句子表示
Tree-Structured LSTMs
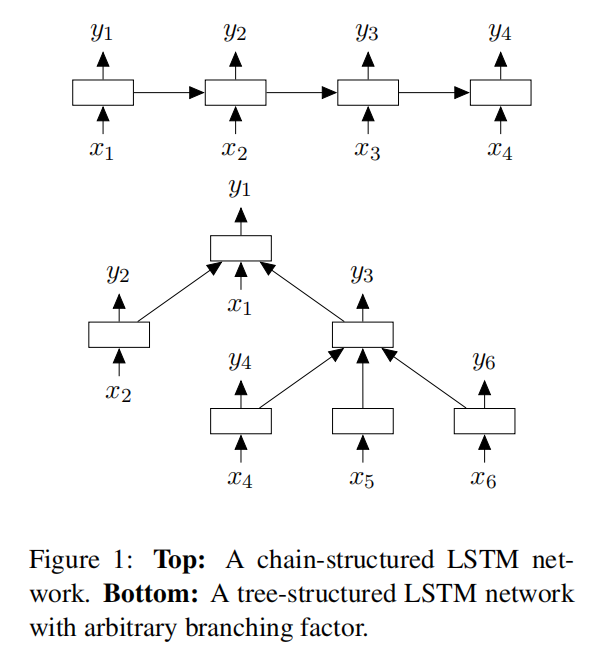
两种模型都能够处理树型结构的输入,标准的LSTM含有输入门 $i_j$ 和输出门 $o_j$ ,记忆单元 $c_j$ 和隐藏状态 $h_j$
标准的LSTM和树型LSTM之间的区别在于门向量和记忆单元向量的更新要基于多个child units,前者只需要从上一时刻筛选出信息,而后者需要从多个孩子节点筛选出信息
Child-Sum Tree-LSTMs (Dependency Tree-LSTMs)
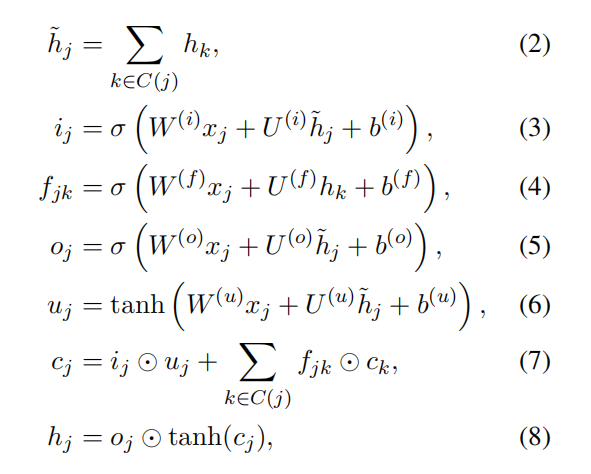
第一个方程直接将所有孩子节点的隐藏状态求和,第三个方程就是和标准的LSTM不同,$f_{jk}$ 表示对于 j 节点的每一个孩子节点 k ,都会生成一个遗忘门,用于筛选对应孩子节点的信息
其中, $k∈C(j)$ , $x_j$ 为输入, $h_k$ 为第 k 个孩子节点的隐藏状态。对于第二行的公式,在依赖树中,模型会学习得到参数 $W(i)$ 使得当该词汇比较重要的时候会输入门 $i_j$ 的值接近1
由于该模型是直接将孩子节点的隐藏状态求和,因此,非常适合于分支因子比较大,或者孩子节点是无序的情况
N-ary Tree-LSTMs (Constituency Tree-LSTMs)
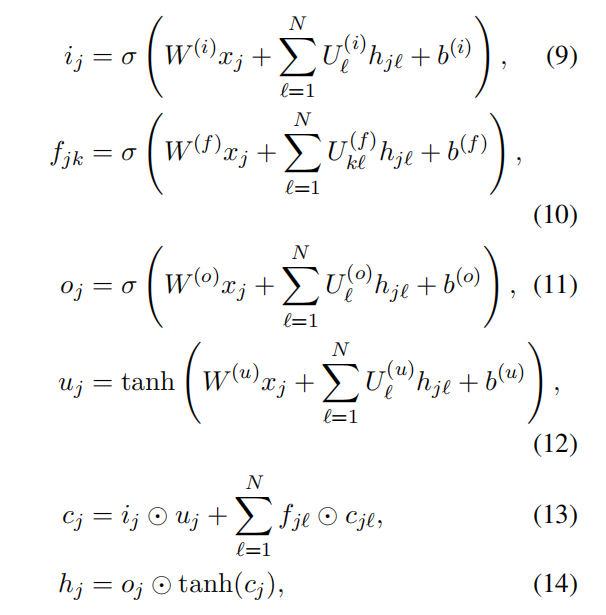
该模型适用于分支因子最大为 N 的情况,而且孩子节点有序,比如说,孩子节点可以被从1到N进行索引,对于节点 j ,假设第 k 个孩子节点的隐藏状态和记忆单元分别为 $h_{jk}$ 和 $c_{jk}$
其中, k=1,2,…,N 。该模型对每个孩子 k 都使用的单独的参数,由此,使得该模型能够学习到孩子节点更加细微的状态
对于第二行的遗忘门参数,模型定义了第 k 个孩子的遗忘门 $f_{jk}$ ,参数包含非对角的参数矩阵 $U_{kℓ}^{(f)}$ , $k≠ℓ$ 。这个参数使得能够更加细微地控制从孩子节点传递信息到双亲节点。对于比较大的 N 值,这些参数量会非常大,在这种情况下直接固定其参数或者置为零
Models
Tree-LSTM Classfication
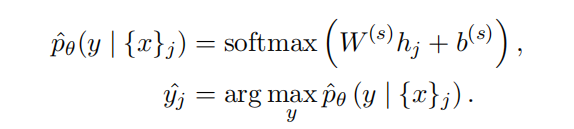
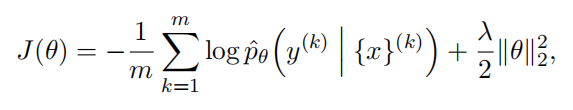
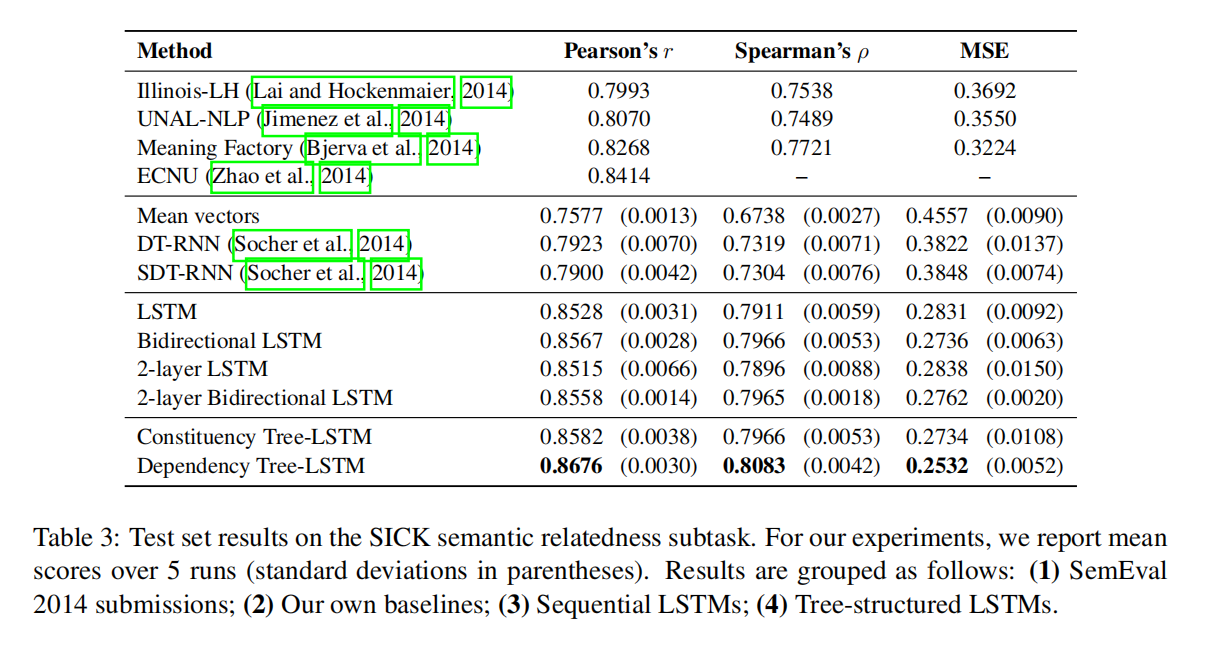
Semantic Realatedness of Sentence Pairs
给定一个句子对,模型需要预测出一个实数值的相似度score,范围为 [1,K] ,其中, K>1 是一个整数,分数越高,表示相似度越大。
模型首先产生两个句子的representation, $h_L$ 和 $h_R$ ,然后使用这两个向量预测出相似度score $\hat{y}$ ,同时考虑两个向量的距离和角度:
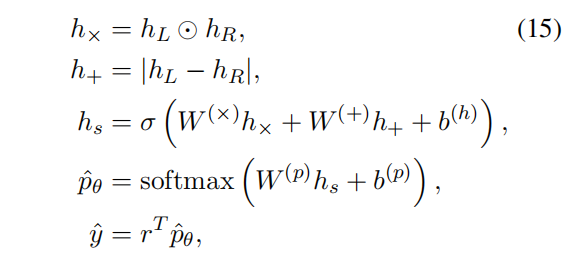
其中, $r^T=[12…K]$
Experiments