LoRA:秩分解矩阵低成本微调
Abstract
自然语言处理的一个重要范例包括对一般领域数据进行大规模的预训练和对特定任务或领域的适应。本文提出Low-Rank Adaptation or LoRA,冻住原本预训练模型的参数,注入可训练的秩分解矩阵。与使用Adam进行微调的GPT-3 175B相比,LoRA可以减少可训练参数的数量10000倍,GPU内存需求减少3倍。LoRA在RoBERTa、DeBERTa、GPT-2和GPT-3上的性能相当或更好,尽管它具有更少的可训练参数、更高的训练吞吐量,而且与适配器不同的是,没有额外的推理延迟
Introduction
微调需要调整整个模型参数,这带来了很大不便性
现存的一些方法寻求使用一些参数或扩展模块来适应新任务,但是往往会因为加深了模型带来新的推理延迟,或是减少了模型可用的序列长度,更重要的是这些方法往往是性能和效率的一个trade off
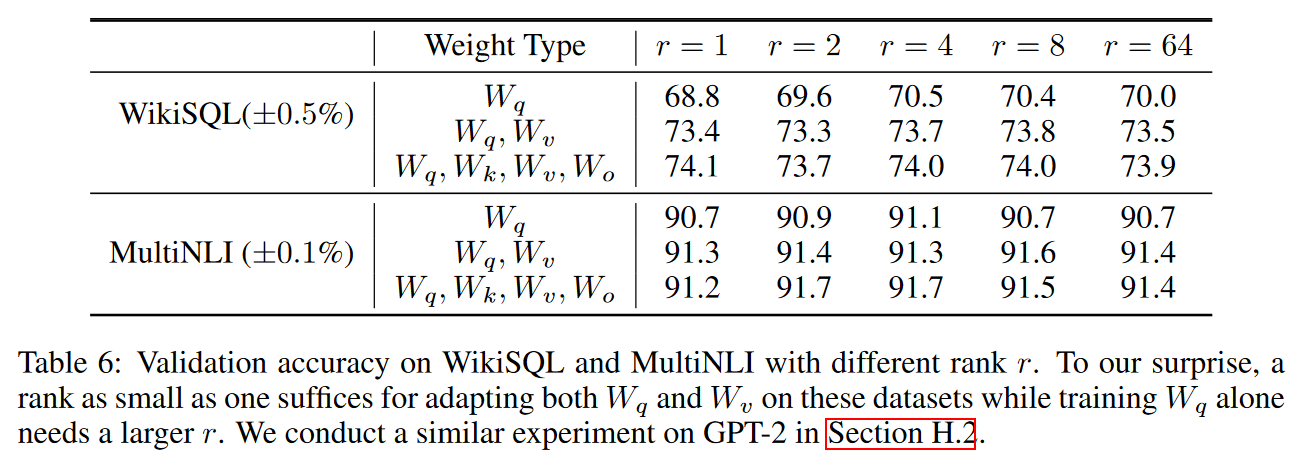
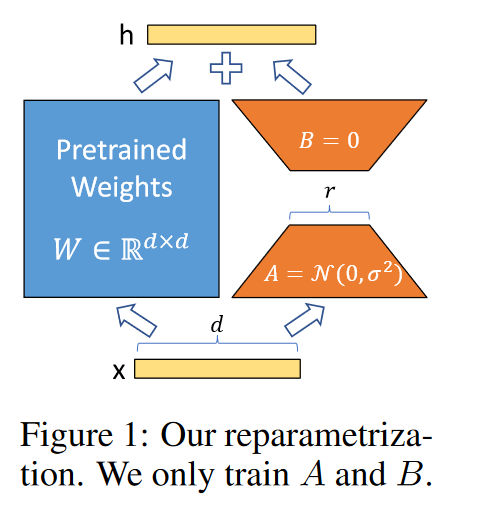
现有研究表明在微调阶段学习到的过度参数化模型实际上存在于一个较低的内在维度上,因此我们假设模型权重的改变事实上是一种low “intrinsic rank”。LoRA允许我们通过优化适应过程中密集层变化的秩分解矩阵来间接训练神经网络中的一些密集层,同时保持预先训练的权值冻结,如图1所示。以GPT-3 175B为例,证明了即使完整的秩(即d)高达12288,一个非常低的秩(即图1中的r可以是1或2)就足够了,这使得LoRA都具有存储和计算效率
LoRA主要有以下的贡献:
- 一个预先训练过的模型可以被共享,并用于为不同的任务构建许多小型的LoRA模块。我们可以通过替换图1中的矩阵A和矩阵B来冻结共享模型并有效地切换任务,从而显著地减少了存储需求和任务切换开销
- 高效,降低硬件要求
- 简单的线性设计可以把可学习的矩阵和冻结的权重在推理部署的时候合并起来
- 可以和别的现有方法正交结合的
Terminologies and Conventions
Transformer的input和output维度是 $d_{model}$ ,$W_q,W_k…$ 等是query/key…等的投影矩阵,$W$ 和 $W_0$ 表示预训练的权重矩阵和累计梯度更新的 $\Delta W$ ,用 $r$ 表示LoRA模块的rank
Problem Statement
对于GPT这样的full fintune而言,目标如下
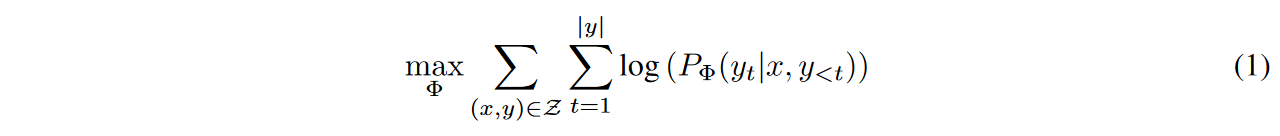
而使用LoRA后可训练参数小于原本的0.01%
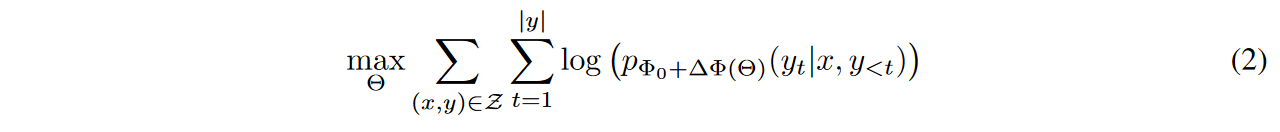
Aren’t Existing Solutions Good Enough?

以语言建模为例,在有效的适应方面,有两种突出的策略:添加adapter layer或优化某些形式的输入层激活
- Adapter Layers Introduce Inference Latency
- Directly Optimizing the Prompt is Hard
Our Method
Low-Rank-Parameterized Update Matrices
假设权重的更新在适应过程中也有一个较低的“intrinsic rank”,对于预训练的权重矩阵 $W_0 \in \mathbb{R}^{d\times k}$ ,我们约束更新分解为 $W_0 + \Delta W=W_0+BA$ ,这里 $B\in \mathbb{R}^{d\times r}, A\in \mathbb{R}^{r\times k}$ ,rank $r<< min(d,k)$ ,其中 $W_0$ 是冻住不接受梯度更新的
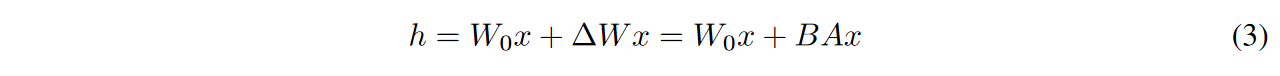
对于A用高斯初始化,对B用0做初始化。用 $\frac{\alpha}{r}$ 来scale $\Delta Wx$ ,在Adam优化的时候,调整 $\alpha$ 和调整学习率是粗略等价的效果
A Generalization of Full Fine-tuning
LoRA不需要更新的权重矩阵在adapt的过程中具有满秩
No Additional Inference Latency
切换下游任务时只需要合并一个新的BA矩阵就行
Applying LoRA to Transformer
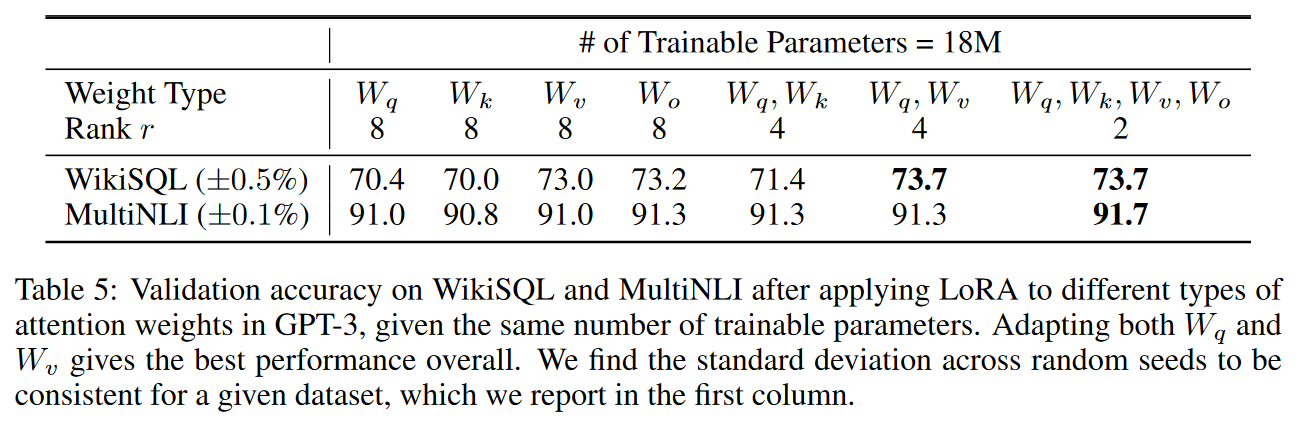
为了简单性和参数效率,将研究限制在只调整下游任务的注意力权重(attention weights),并冻结MLP模块
Practical Benefifits and Limitations
最大的好处是减少了计算和内存开销
Empirical Experiments