论文地址:E(n) Equivariant Graph Neural Networks
EGNN:等变图神经网络
Abstract
EGNN不需要再中间层计算high-order表示仍然有很好的效果,现有的方法大多限制在三维空间中等变,而本文的方法可以扩展到更高维
Introduction
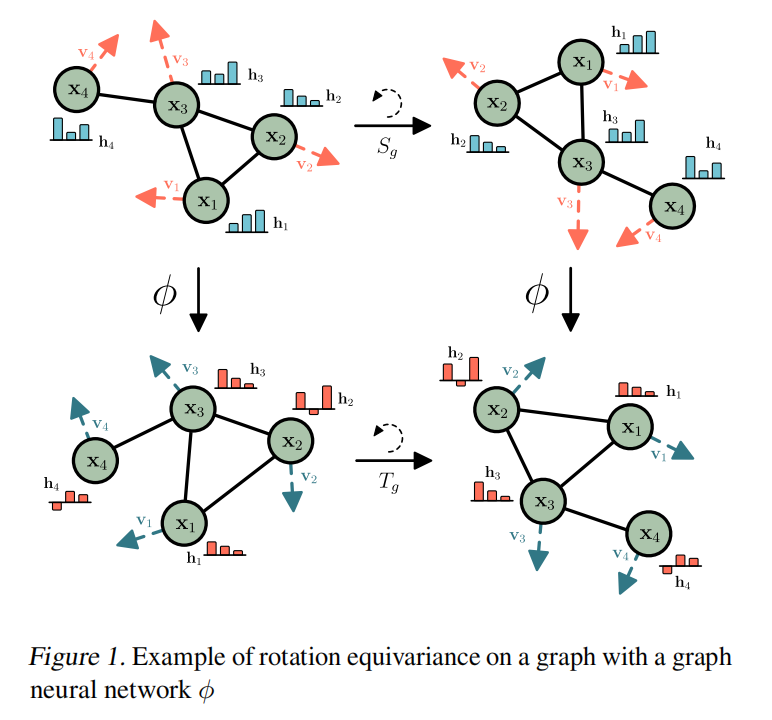
虽然深度学习已经在很大程度上取代了手工制作的特征,但许多进展都严重依赖于深度神经网络中的归纳偏差
许多问题表现出三维平移和旋转对称性,例如点云(point clouds)、三维分子结构(3D molecular structures)和N体粒子模拟(N-body particle simulations)。与这些对称性对应的群被称为欧几里德群:SE(3),当包括反射时为E(3)。通常希望在这些任务上的预测是关于E(3)变换等变的或不变的。
许多工作在研究中间网络层的高阶表示类型方面取得了创新。然而,这些高阶表示的变换需要花费大量代价计算系数或近似值。
于是,本文提出了一种新的体系结构,它是平移、旋转和反射等变的E(n),并且对于输入点集是排列等变的。同时模型比以前的方法更简单,并且模型中的等变性不仅限于三维空间,可以扩展到更大维度的空间而没有显著增加计算量
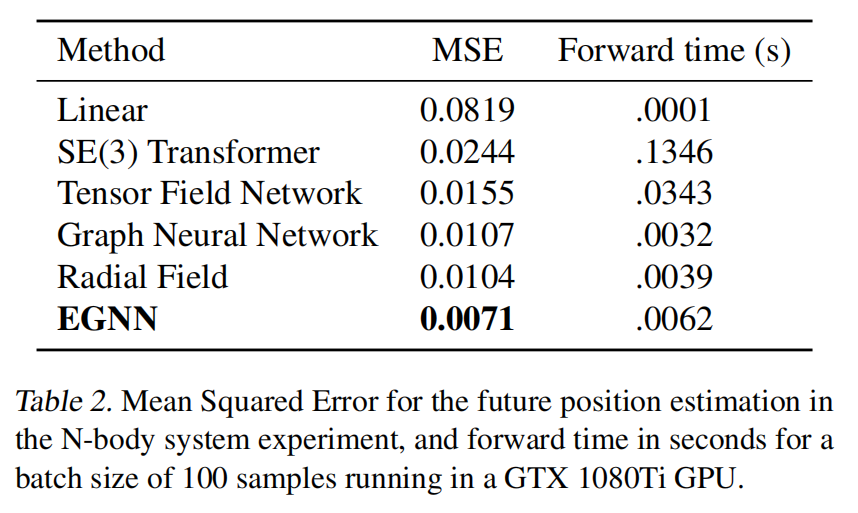
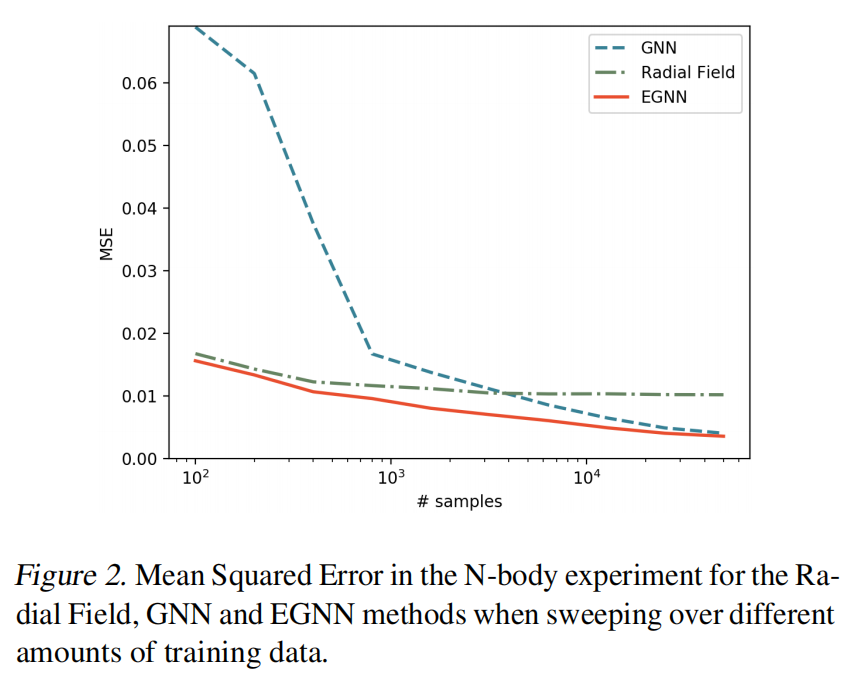
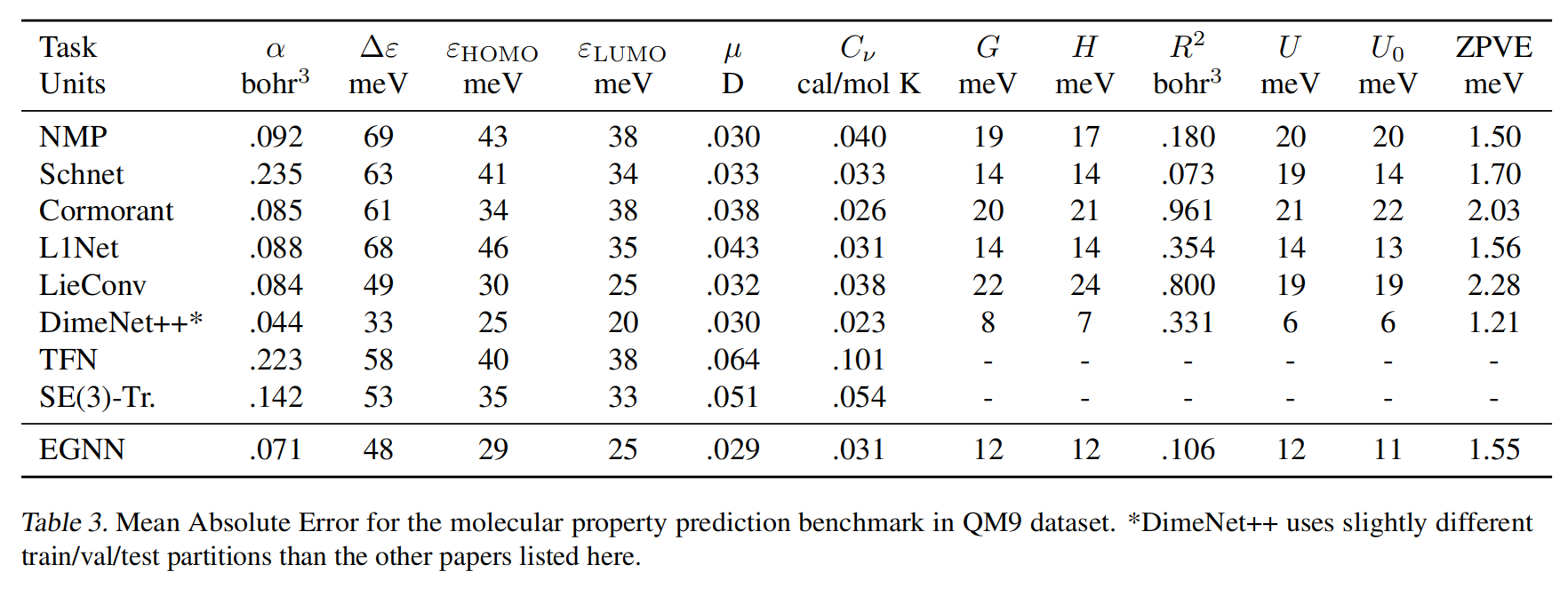
文章采用QM9数据集。QM9数据集由表示为原子集合的小分子组成(每个分子最多有29个原子),每个原子具有与之关联的三维位置和描述原子类型的五维独热编码节点嵌入(one-hot node embedding)(H,C,N,O,F)。数据集标签是每个分子的多种化学性质,通过回归进行估算。这些性质对于原子位置上的平移、旋转和反射是不变的。因此,对于这个任务来说,E(3)不变的模型非常适合。
Background
Equivariance
三种等变性质,$y=\phi(x)$
- 平移等变性
- 将输入集合平移 $g\in R^n$ 会导致等效平移的输出。记 $x+g$ 为 $(x_1+g,…,x_M+g)$ 。然后 $y+g=\phi(x+g)$
- 旋转(和反射)等变性
- 对于任意的正交矩阵 $Q\in R^{n\times n}$ ,记 $Qx$ 为 $(Qx_1,…,Qx_M)$。那么旋转输入将导致输出的等效旋转 $Qy=\phi(Qx)$
- 排列等变性
- 对于输入进行排列将导致输出的相同排列 $P(y)=\phi(P(x))$,其中P是一个再行索引上进行的排列
Graph Neural Networks
图神经网络是对图结构数据进行操作的置换等变网络,给定一个图 $G=(V,E)$,其中节点 $v_i\in V$,边 $e_{ij}\in E$
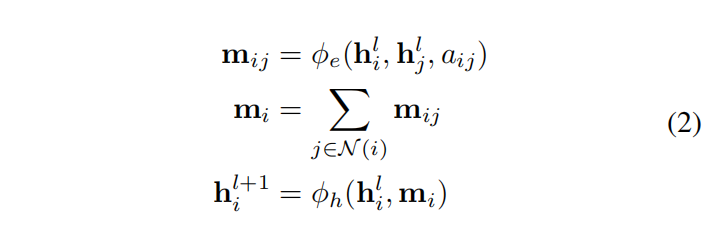
其中 $h_i^l\in R^{nf}$ 表示层 $l$ 中节点 $v_i$ 的 $nf$ 维嵌入,$a_{ij}$ 是边属性,$N(i)$ 表示节点 $v_i$ 的邻居集合。最后,$\phi_e$ 和 $\phi_h$ 分别是常用的多层感知机(MLP)近似的边和节点操作
Equivariant Graph Neural Networks
给定一个图 $G=(V,E)$,其中节点 $v_i\in V$,边 $e_{ij}\in E$。除了节点特征嵌入 $h_i^l\in R^{nf}$,同时考虑与每个图节点相关的n维坐标 $x_i\in R^n$ 。模型将保持对这组坐标 $x_i$ 的旋转和平移的等变性,并且它将像GNN一样保持对节点集合V的排列的等变性
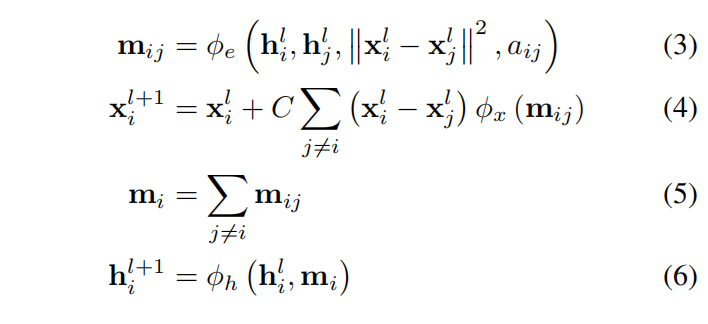
上述提出的方法与方程2中的原始图神经网络的主要区别可以在方程3和4中找到。C为 $\frac{1}{M-1}$
Related Work

Experiments