DyMEAN:端到端影子互补桥接抗体抗原
Abstract
介绍了一种名为 dynamic Multi-channel Equivariant grAph Network (dyMEAN) 的新模型,它是一个 端到端(end-to-end) 的 全原子(full-atom) 抗体设计方法。该方法的主要目标是改进现有的 基于学习的抗体设计 方法,解决以下两个主要问题:
- 现有方法的局限性:
- 现有的学习方法通常仅关注抗体设计流程的某个子任务,使得整体方案次优或资源消耗过大。
- 这些方法要么忽略抗体的框架区(framework regions),要么忽略侧链(side chains),无法完整捕捉抗体的全原子几何信息。
- dyMEAN 的解决方案:
- 端到端建模:dyMEAN 可直接处理 仅提供抗原表位(epitope)和部分抗体序列(incomplete sequence) 的问题,而无需多阶段流水线。
- 结构初始化:使用结构知识进行初始结构猜测(structural initialization)。
- 影子互补位(shadow paratope):提出影子互补位来桥接抗原-抗体的交互信息。
- 多通道等变编码器(adaptive multi-channel equivariant encoder):该编码器可以在全原子建模时,适应不同残基的原子数目变化,同时更新 1D 序列和 3D 结构。
- 最终对接(docking):通过对齐影子互补位,完成抗原-抗体的结合结构预测。
- 实验验证:
- 通过在 CDR-H3 设计(epitope-binding CDR-H3 design)、复合结构预测(complex structure prediction) 和 亲和力优化(affinity optimization) 三个任务上的实验,验证了 dyMEAN 在 端到端框架和全原子建模 方面的优越性。
Introduction
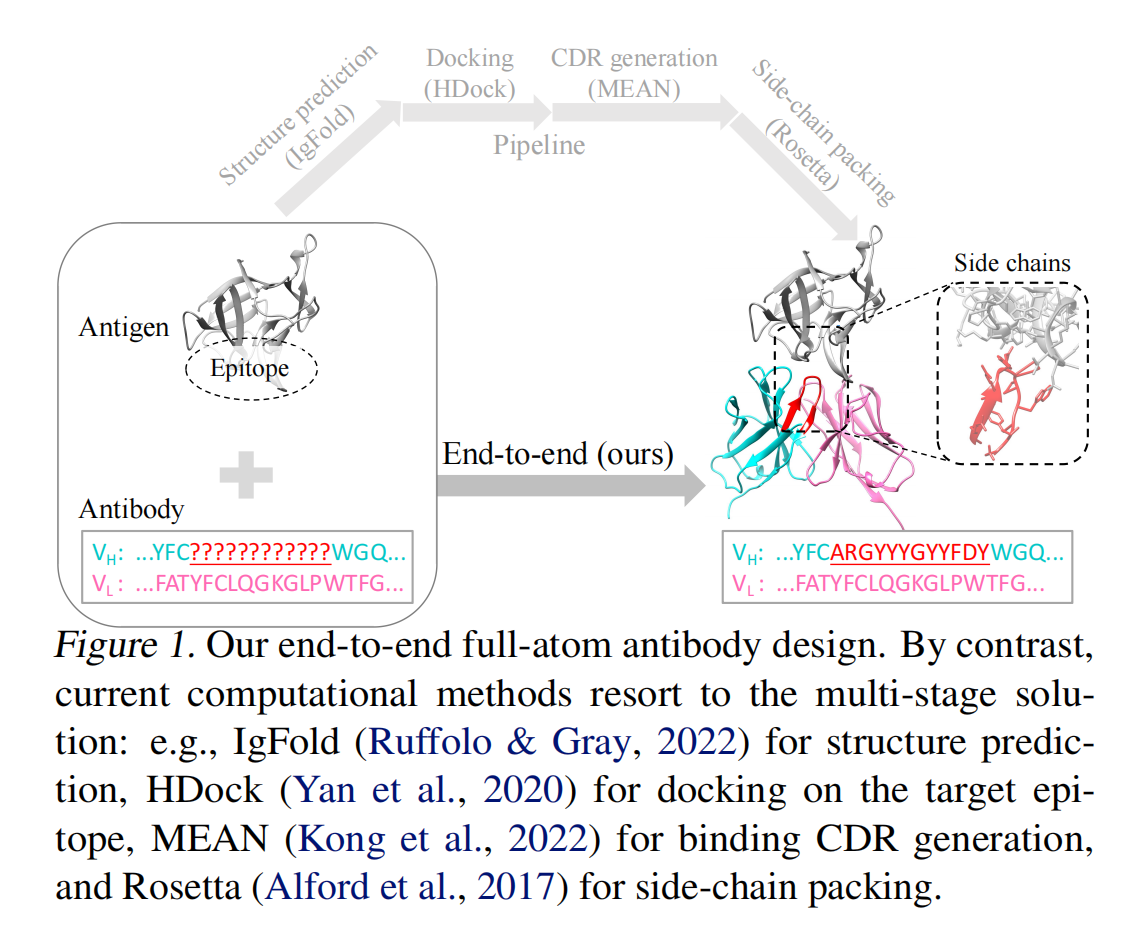
本文研究的是 抗体设计(antibody design),其在 治疗学(therapeutics) 和 生物学(biology) 领域具有重要应用。然而,抗体设计仍然是一个极具挑战性的任务,主要原因包括 互补决定区(CDRs) 的高变异性以及抗原-抗体相互作用规律的复杂性。
近年来,虽然计算方法在抗体设计方面取得了一些进展,但仍然存在两大核心问题:
- 现有方法多采用多阶段流水线(pipeline-based approach),结构预测、docking、CDR生成、side-chain packing,缺乏整体优化,导致结果次优或计算开销大。
- 缺乏全原子级别的建模(full-atom modeling),导致对抗原-抗体复合物结构的描述不够精确。
本文提出了一种新的 端到端全原子抗体设计模型——dyMEAN(dynamic Multi-channel Equivariant grAph Network),以克服上述问题。该模型直接从 抗原表位(epitope) 和 不完整抗体序列(incomplete antibody sequence) 生成完整的 1D 序列和 3D 结构,并通过 影子互补位(shadow paratope) 机制以及 E(3)-等变(E(3)-equivariance) 编码器提高抗体设计的准确性和对接(docking)精度
现有计算方法的不足
- 基于能量优化的方法采用统计能量函数(如 Rosetta)优化抗体结构,但能量函数的表达能力有限,难以准确建模抗体-抗原相互作用。
- 训练 语言模型(Language Models, LMs) 仅使用抗体的 1D 序列 进行优化,由于缺乏 结构信息(3D Geometry),序列生成效果受限。
- 基于深度生成模型的序列-结构联合设计可以同时生成 CDR 序列和 3D 结构 有上下文建模不完整等问题
为了克服上述问题,本文提出 dyMEAN(dynamic Multi-channel Equivariant grAph Network),其特点如下:
-
直接从 抗原表位(epitope) 和 不完整抗体序列 生成 完整的抗体序列和 3D 结构,不依赖多阶段流水线,避免误差累积,减少计算资源消耗。
-
通过 保守残基(conserved residues) 生成 抗体框架区(framework regions)的初始结构。
-
在抗原表位附近创建影子互补位(shadow paratope),它:
- 共享 真实 CDR-H3 的 隐藏状态。
- 独立优化坐标,保证 抗体-抗原相互作用不依赖抗体初始位置
-
自适应多通道等变编码器
-
采用 E(3)-等变(E(3)-equivariant) 机制,同时更新 1D 序列和 3D 结构。
-
处理 不同残基的可变原子数,支持 全原子建模(Full-Atom Modeling)。
-
-
通过影子互补位 对齐真实 CDR-H3,实现抗体对接,生成最终的抗原-抗体复合物
Notations and Definitions

抗体(Antibody)是一种 Y 形对称蛋白质,由两个相同的链组成,每条链包括:
- 重链(Heavy Chain, VH)
- 轻链(Light Chain, VL)
每条链由 多个恒定域(Constant Domains) 和 一个可变域(Variable Domain) 组成:
- 恒定域(Constant Domains) 在不同抗体中保持不变。
- 可变域(Variable Domains) 负责 特异性结合不同的抗原,是抗体设计的核心关注点。
本文中,我们使用 $V_H$ 和 $V_L$ 分别表示 重链(VH)和轻链(VL)的可变域。可变域由 四个框架区(Framework Regions, FRs) 和 三个互补决定区(Complementarity Determining Regions, CDRs) 交替排列构成
抗体的结合区域称为互补位(Paratope),而抗原的结合区域称为表位(Epitope),本文中,互补位专指 CDR-H3,因为它在抗原结合中起着主导作用
-
抗体和抗原的图表示
- 抗原表位图(Epitope Graph):$G_E(V_E,E_E)$
- 抗体图(Antibody Graph):$G_A(V_A,E_A)$
-
残基的特征表示
- 氨基酸类型 $s_i$:残基的氨基酸种类(如 Ala、Ser、Glu)。
- 多通道3D坐标矩阵 $X_i\in \mathbb{R}^{3\times c_i}$
- $c_i$ 代表该残基得原子数(包括主链和侧链)
- 由于不同氨基酸的侧链结构不同,$c_i$ 不固定
- 为了兼容不同残基的原子数,dyMEAN 采用 多通道表示
-
图的边构造
-
dyMEAN 采用 k-近邻(kNN) 机制来构造图的边,计算两个残基 $v_i$ 和 $v_j$ 之间的最小成对原子距离:
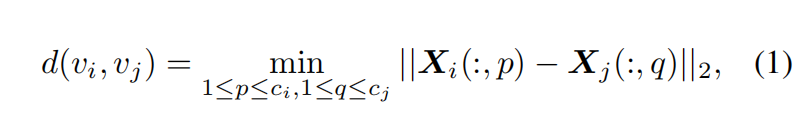
其中:p和q表示原子坐标
-
-
此外还在重链、轻链和抗原表位上增加了三个全局节点
Task Definition
输入 抗原表位 + 部分抗体序列,预测 完整的 CDR-H3 序列和 3D 结构,预测结果应能 正确对接到抗原表位。
Our Method: dyMEAN
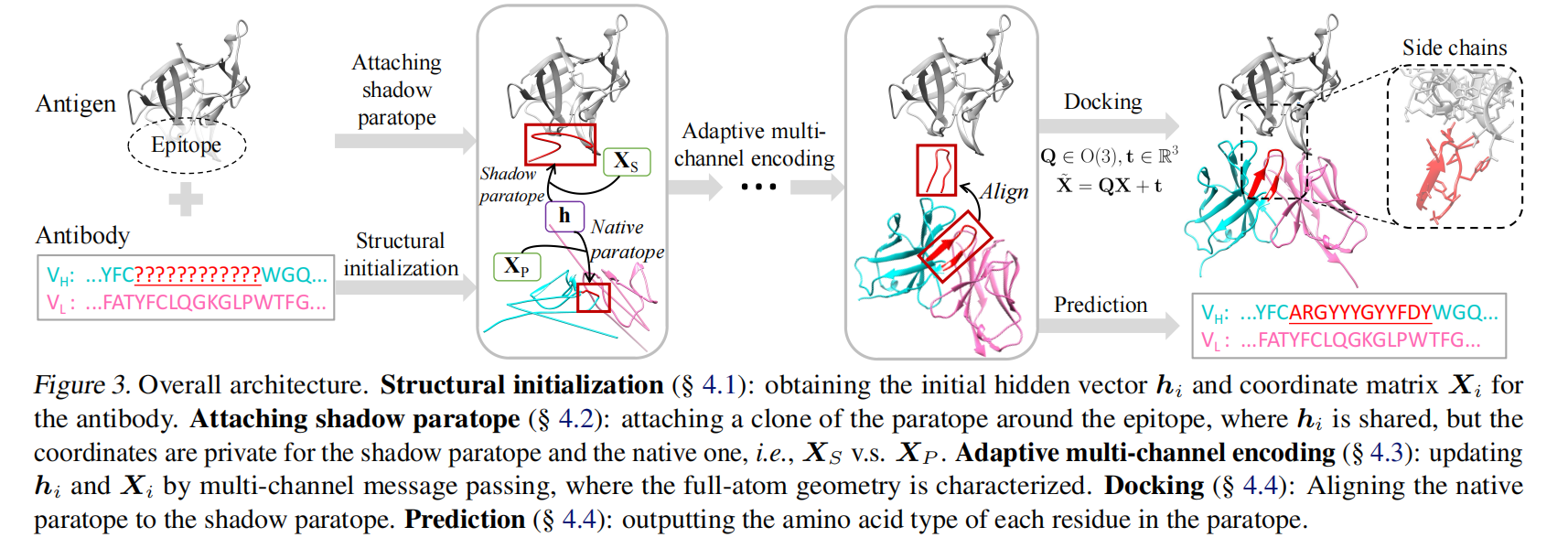
每个顶点(来自抗原表位图 $G_E$ ,抗体图 $G_A$ 以及互补位子图 $G_P$ )被赋予:
- 一个 不变向量(invariant vector) $h_i\in\mathbb{R}^d$
- 一个 等变坐标矩阵(equivariant coordinate matrix) $X_i\in\mathbb{R}^{3\times c_i}$
总体流程可以表示为:
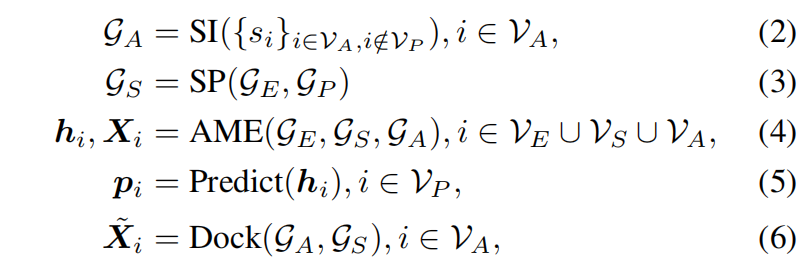
其中:
- SI(Structural Initialization,结构初始化):
- 通过已知的 不完整抗体序列 预测 初始坐标 $X_i^{(0)}$ 和隐藏状态 $h_i^{(0)}$
- SP(Shadow Paratope,影子互补位):
- 在 抗原表位 和 互补位 之间引入 影子互补位 $G_S$,该影子互补位共享 CDR-H3 的隐藏状态,连接抗原和抗体,为 docking 提供锚点。
- AME(Adaptive Multi-channel Encoder,自适应多通道编码器):
- 迭代更新所有顶点的 隐藏状态 $h_i$ 和坐标 $X_i$
- 预测模块(Prediction):
- 计算 **CDR-H3 氨基酸分布 ** $p_i$
- 对接模块(Docking):
- 通过 对齐影子互补位 $G_S$ 完成抗体-抗原结合。
Structural Initialization with Conserved Residues
在输入数据中,抗体序列 ${s_i}_{i\in V_A,i\notin V_P}$ 缺失了 CDR-H3 信息,同时 3D 结构未知。因此,dyMEAN 需要初始化 抗体隐藏状态 $h_i^{(0)}$ 和3D坐标 $X_i^{(0)}$
隐藏状态初始化 $h_i^{(0)}$
每个残疾的隐藏状态是氨基酸类型+位置编码得到,$h_i^{(0)}=f(s_i,r_i)=f_{s_i}+f_{r_i}$,对于缺失的 CDR 区域,dyMEAN 会用一个特殊类型 [MASK] 来表示这些残基。
初始化 3D 坐标 $X_i^{(0)}$
框架区(FRs)通常是保守的,因此,dyMEAN 使用 已知抗体结构中框架区的坐标 来初始化抗体的 3D 坐标 ($X_i^{(0)}$),具体步骤如下:
- 对齐保守残基:
- 通过对比 抗体序列 和 结构数据库中的抗体序列,识别出在多个抗体中都保持一致的残基,这些被认为是保守的残基。
- 通过抗体编号系统(如 IMGT 编号系统) 对抗体序列进行比对,找到 在超过 95% 的抗体中类型一致的残基。
- Kabsch 对齐算法:
- 使用 Kabsch 算法 将 框架区的保守残基 的 主链原子(backbone atoms) 进行对齐,从而得到这些保守残基的平均 3D 坐标。
- 得到的坐标将用于初始化 框架区的 3D 坐标。
- 插值和扩展:
- 对于框架区中的非保守残基,dyMEAN 通过 线性插值 将其坐标值插入到保守残基之间。对于位于链两端的残基,通过从最近的保守残基开始,进行 向外的线性插值。
坐标的标准化
完成坐标初始化后,dyMEAN 会对 坐标进行标准化:
- 对所有抗体的坐标进行 3D 平移,确保它们的 均值为 0。
- 1D 方差标准化:对所有抗体的坐标进行 1D 方差标准化,确保不同抗体之间的尺度一致。
通过这种方式,dyMEAN 使用保守残基的结构信息为 框架区 提供了一个 合理的初始结构猜测。这为后续的 影子互补位(shadow paratope) 建立和 多通道消息传递(multi-channel message passing) 打下了基础
E(3)-Invariant Attachment of Shadow Paratope
在 dyMEAN 方法中,为了增强抗体与抗原之间的信息交换,研究者提出了Shadow Paratope(影子互补位点)的概念。它是一种在抗原的表位(epitope)附近附加的伪互补位点副本,主要具有两个关键作用:
- 传递 E(3)-不变(E(3)-invariant)信息:影子互补位点与原始互补位点共享相同的隐藏状态 $h_i$ 和拓扑结构,从而在抗原与抗体之间进行信息交换,而不依赖于抗体的初始位置。
- 作为关键对接点:影子互补位点将在抗体与抗原的对接过程中(详见 §4.4)发挥关键作用。
值得注意的是,由于影子互补位点仅交换 E(3)-不变的信息(即隐藏状态 $h_i$),而不是坐标 $X_i$,因此其 3D 坐标和最终对接结构不会受到抗体初始位置的影响。这种特性确保了 dyMEAN 方法的通用性和鲁棒性。
影子互补位点的构造
影子互补位点由一个子图 $G_s=(V_S,E_S)$ 表示,其中“
- 顶点集 $V_S$ 包含影子互补位点的残基
- 边集 $E_S$ 分为两部分:
- 内部边:直接复制自原始互补位点之间的连接。
- 外部边:用于连接影子互补位点和抗原表位(epitope)。
对任意表位残基 $v_i \in V_E$ 和影子互补位点 $v_j \in V_S$,其外部边根据k 近邻(kNN)距离构造:
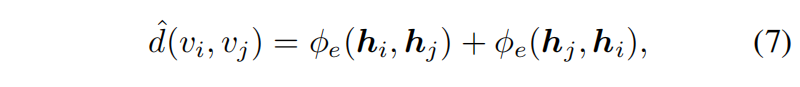
其中,$\varphi_e$ 是一个多层感知机(MLP, Multi-Layer Perceptron),用于学习特定的距离表示。
影子互补位点的初始化
- 影子互补位点的隐藏向量 $h_i$ 是从原始互补位点复制而来,以保证一致性。
- 影子互补位点的坐标 $X_i$ 按照标准高斯分布 $N(0, I)$ 在表位中心附近初始化,确保在训练初期的随机性,同时不会破坏最终的 E(3)-不变性。
最终,影子互补位点子图 $G_S$ 被合并到表位图 $G_E$ 中,从而构建一个新的图结构 $G_E \cup G_S$,用于后续的消息传递和抗体对接
Adaptive Multi-Channel Equivariant Encoder
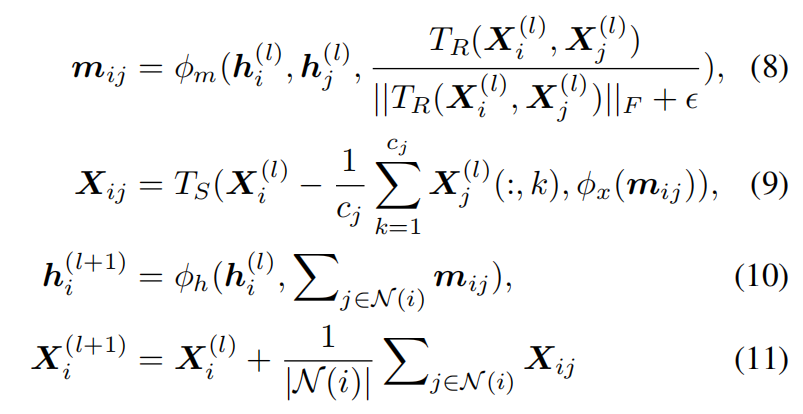
Geometric Relation Extractor $T_R$
-
计算通道级别的欧几里得距离,给定 $X_i\in\mathbb{R}^{3\times c_i}$ 和 $X_j\in\mathbb{R}^{3\times c_j}$ ,对于每个通道(每个原子)都计算 $D_{ij}(p, q) = ||X_i(:, p) - X_j(:, q)||_2$
-
计算加权相关性
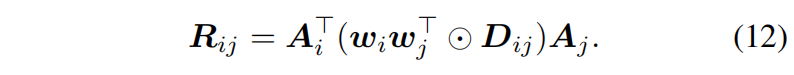
其中 $w_{i}\in\mathbb{R}^{c_i\times 1}$ 和 $w_{j}\in\mathbb{R}^{c_j\times 1}$ , $A_{i}\in\mathbb{R}^{c_i\times d}$ 和 $A_{j}\in\mathbb{R}^{c_j\times d}$
最后的 $R_{i,j}\in\mathbb{R}^{d\times d}$ 保持固定维度,确保输入的维度一致
Geometric Message Scaler, $T_S$
$T_S$ 负责 调整几何信息的尺度,确保不同残基的坐标信息能有效地传递和融合,坐标 $X\in\mathbb{R}^{3\times c}$ ,非几何信息 $s=\phi_x(m_{ij})\in\mathbb{R}^C$,其中C是通道数的上界大小,$T_S(X,s)$ 如下计算:
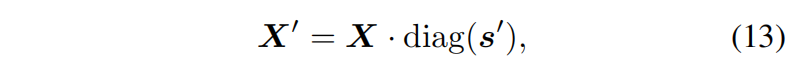
其中 $s’\in\mathbb{R}^c$ 是 s的平均池化,window size C-c+1,stride=1,diag(·)是矩阵的对角元素
Information Exchanging between $G_E$ and $G_A$
抗原表位图 $G_E$ 和 抗体图 $G_A$ 是初始状态下不直接连接的,但模型需要在二者之间进行有效的信息交换,以优化 抗体-抗原结合(docking)。为了解决这个问题,dyMEAN 通过影子互补位(Shadow Paratope, $G_S$) 进行信息传递
- 第一阶段(Antibody Graph $G_A$ 处理)
- 先在 抗体图 $G_A$ 上运行 1 层 AME(1-layer AME)。
- 将计算得到的隐藏向量 $h_i$ 从抗体互补位(Paratope $G_P$)复制到影子互补位(Shadow Paratope GSG_SGS),使得 GSG_SGS 具有抗体互补位的关键信息。
- 第二阶段(Epitope Graph $G_E$ 与 Shadow Paratope $G_S$ 处理)
- 在 联合图 $G_E \cup G_S$ 上运行 1 层 AME,交换抗原表位和影子互补位之间的信息。
- 将影子互补位 $G_S$ 的隐藏向量 $h_i$ 反向复制回抗体互补位 $G_P$,使抗体获得抗原表位的信息。
- 重复交替计算
- 上述两步 交替执行 LLL 层,在抗原和抗体之间反复交换信息,确保二者的交互信息逐渐收敛。
- 之后,在 抗体图 $G_A$ 上额外执行 1 层 AME,以将更新的信息传播到整个抗体结构中。
dyMEAN 采用的 几何关系提取器(Geometric Relation Extractor, TR) 和 几何消息缩放器(Geometric Message Scaler, TS) 具有以下等变性属性:
- TR 是 $E(3)$-不变(E(3)-Invariant):保证了计算的几何关系在旋转、平移、反射下保持不变。
- TS 是 $O(3)$-等变(O(3)-Equivariant):确保在任何旋转下,消息传递保持等变性。
- 信息交换过程 $G_E ↔ G_A$ 通过 $G_S$ 进行,并且是 $E(3)$-不变的。
Prediction, Docking and Training Losses
Prediction
dyMEAN 采用 逐步全镜头解码策略(progressive full-shot decoding strategy) 进行 CDR-H3 1D 氨基酸序列 和 3D 结构 预测,并在 T 轮迭代中逐步优化:
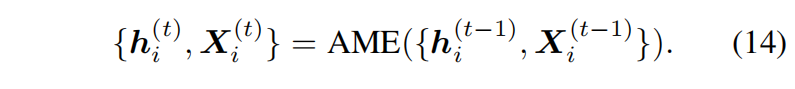
dyMEAN 使用 多层感知机(MLP, Multi-Layer Perceptron) 进行 CDR-H3 的氨基酸预测:
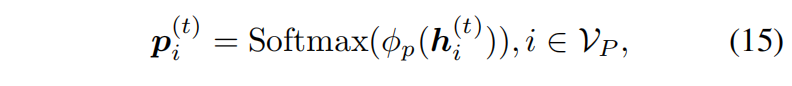
隐藏状态 $h_i^{(t)}$ 在每轮迭代后都会更新:
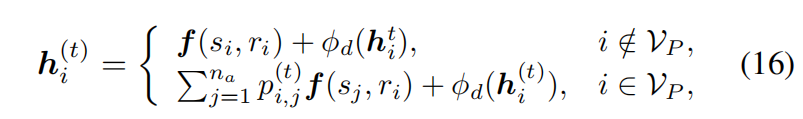
其中 $f(s_i,r_i)=f_{s_i}+f_{r_i}$ 是抗体序列的嵌入,$p_i^{(t)}(j)$ 表示 CDR-H3 位置 i 处的氨基酸 j 的概率,$\phi_d(h_i^{(t)})$ 是memory term
每次迭代后,dyMEAN 重新计算 抗体图 $G_A$ 和抗原表位图 $G_E$ 之间的边,以更新其拓扑结构
Docking
最终迭代 结束后,dyMEAN 采用 Kabsch 算法(Kabsch, 1976) 进行抗体-抗原对接:
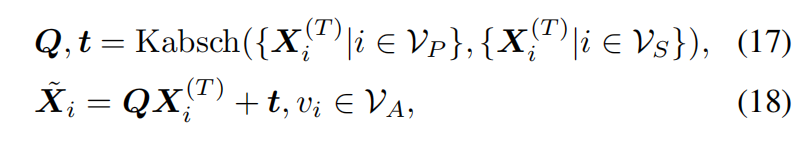
-
影子互补位 GSG_SGS 提供 抗体 CDR-H3 预测结构的参考对接点。
-
Kabsch 对齐的目标 是将 CDR-H3($V_P$)调整到影子互补位($V_S$)的位置,以优化抗原-抗体的对接关系。
Loss Function
使用 交叉熵损失(Cross-Entropy Loss) 监督 CDR-H3 氨基酸预测:
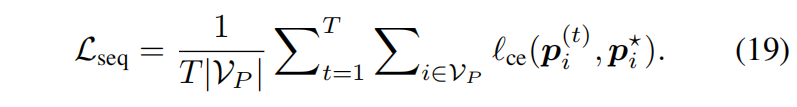
Huber 损失(Huber Loss) 用于训练 最终 3D 坐标:
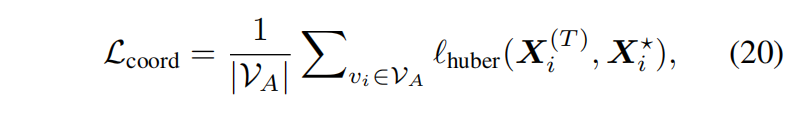
此外,还添加了 化学键长监督损失:
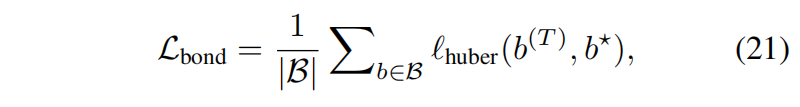
最终的结构损失是两者相加
为了优化 抗体-抗原对接质量,dyMEAN 采用 两个额外损失:
**影子互补位坐标损失 **和 外部距离损失
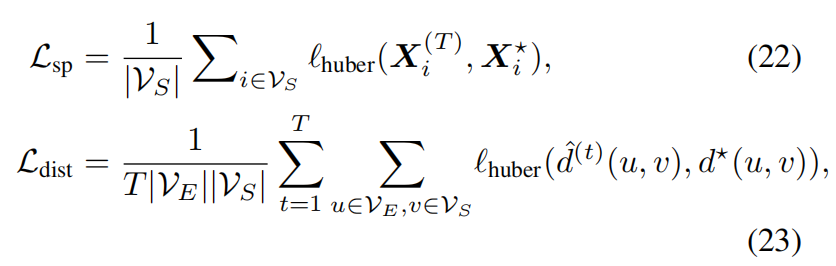
最终的dock损失是两者相加
Experiments
dyMEAN 在 SAbDab 数据集 上训练,并使用 PyTorch 分布式计算框架 进行加速。
2.1. 训练超参数
训练细节
- 优化器:Adam
- 初始学习率:$1 \times 10^{-3}$,指数衰减 到 $1 \times 10^{-4}$。
- 批量大小(Batch Size):16
- 训练轮数(Epochs):
- CDR-H3 设计 & 亲和力优化:200 轮
- 复合物结构预测:250 轮
- 梯度更新策略:采用余弦调度(cosine schedule)降低学习率,以 防止模型过拟合。
Masking 机制
由于 CDR-H3 是主要变异区域,研究者采用 动态 Masking 训练策略:
- 初始阶段:保留 90% 互补位(paratope)残基 不被 Mask。
- 随着训练进行,逐步减少 Mask 率,使最终阶段 所有互补位残基均被 Mask,确保 模型可以在未知残基下生成合适序列。
数据集与实验设定
-
研究者提取了距离抗体最近的 48 个残基 作为抗原表位(epitope),这足以覆盖所有结合残基。
-
由于之前没有
端到端全原子抗体设计(end-to-end full-atom antibody design)的方法,研究者使用了一系列现有的竞争性方法
作为基线:
- IgFold (Ruffolo & Gray, 2022):专门用于抗体结构预测的 AlphaFold 变体。
- HDock (Yan et al., 2020):基于知识评分函数的 docking 方法。
- RosettaAb (Adolf-Bryfogle et al., 2018):基于统计能量函数优化抗体序列和结构。
- MEAN (Kong et al., 2022):基于等变注意力图网络(equivariant attention graph networks)的 CDR-H3 生成方法。
- Diffab (Luo et al., 2022):基于扩散模型(diffusion model)的 CDR 生成方法,并考虑了侧链方向。
- HERN (Jin et al., 2022):一个不需要结构预测、docking 和侧链优化的端到端抗体设计方法,但未考虑框架区建模(framework region modeling)。
Epitope-binding CDR-H3 Generation
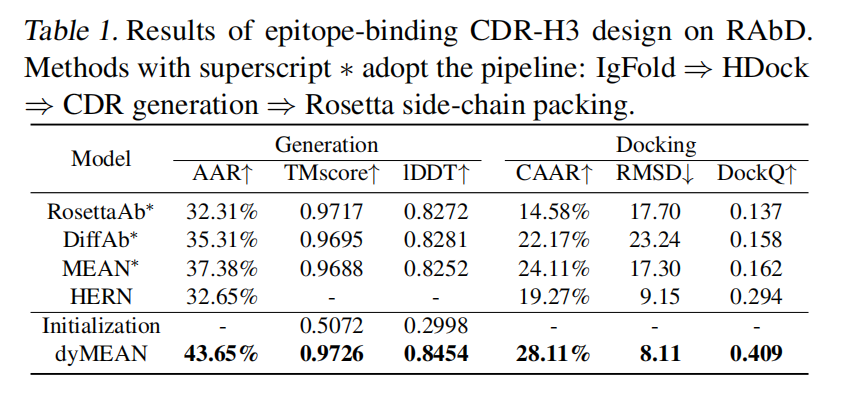
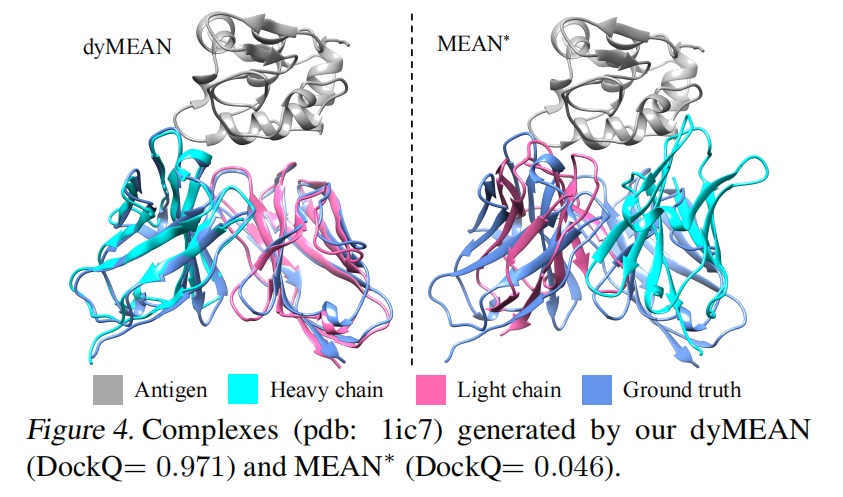
目标:CDR-H3 是抗体中变异性最高 的区域,决定了抗体的结合特异性和亲和力(Raybould et al., 2019)。本实验的目标是预测 CDR-H3 的 1D 序列和 3D 结构。
评估指标
- Amino Acid Recovery (AAR):生成的序列与真实序列的重叠比例。
- Contact AAR (CAAR):仅计算与抗原表位距离小于 6.6Å 的 CDR-H3 残基的 AAR(Ramaraj et al., 2012)。
- TM-score:衡量生成的 CDR-H3 结构与真实结构的全局相似性(Zhang & Skolnick, 2004)。
- Local Distance Difference Test (lDDT):基于原子间距离矩阵 评估生成结构与真实结构的相似性(Mariani et al., 2013)。
- RMSD(Root Mean Square Deviation):计算 CDR-H3 绝对坐标的均方根偏差(未进行 Kabsch 对齐)。
- DockQ:综合衡量 docking 质量的指标(Basu & Wallner, 2016)。
📌 实验结果:
Table 1(CDR-H3 设计结果):dyMEAN 的 AAR = 43.65%,TM-score = 0.9726,lDDT = 0.8454,DockQ = 0.409,在所有指标上均优于基线。
Complex Structure Prediction
目标:在给定 CDR-H3 序列的情况下,预测 整个抗体-抗原复合物的 3D 结构。
评估方法
研究者比较了 dyMEAN 与多个基线方法,包括:
- IgFold⇒HDock(基于 IgFold 预测骨架,再用 HDock 进行 docking)
- IgFold⇒HERN(HERN 进行 docking,再用 Rosetta 预测侧链)
- GT⇒HERN(HERN 直接使用真实结构进行 docking)
- dyMEAN(端到端全原子结构预测)
📌 实验结果(Table 2)
dyMEAN 在所有评估指标上超过基线方法
即使 HERN 使用真实抗体结构(GT⇒HERN),dyMEAN 仍然表现更优,表明其能 有效建模抗体-抗原的相互作用
Affinity Optimization
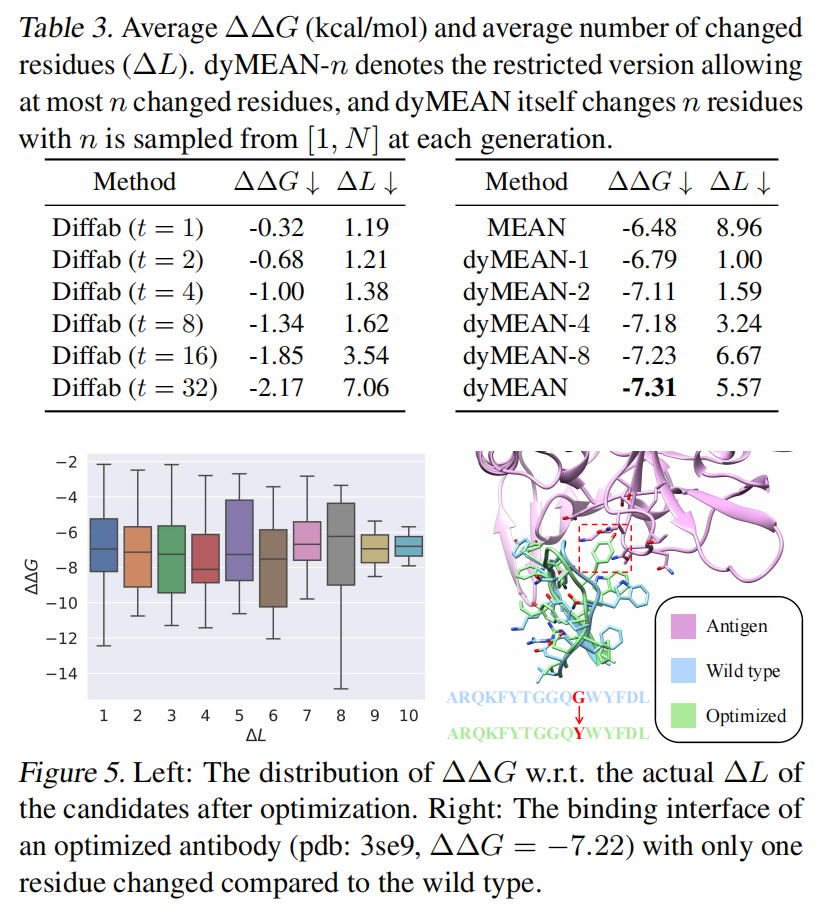
目标:优化抗体的序列,以 最大化与抗原的结合亲和力(binding affinity)。亲和力由 ΔΔG(结合自由能变化) 评估,较低 ΔΔG 代表更好的结合能力。
实验方法
- 使用 GNN-based predictor 计算 ΔΔG(Shan et al., 2022)。
- 采用 FoldX 作为亲和力打分工具。
- 衡量 ΔL(突变残基的数量),以确保优化不会造成过度突变。
📌 实验结果(Table 3)
dyMEAN 在 ΔΔG 下降幅度上优于 MEAN 和 DiffAb,同时保持较低的 ΔL
相比 MEAN(ΔΔG = -5.84,ΔL = 5.09)和 DiffAb,dyMEAN 的亲和力优化能力更强
Analysis
Ablation Study
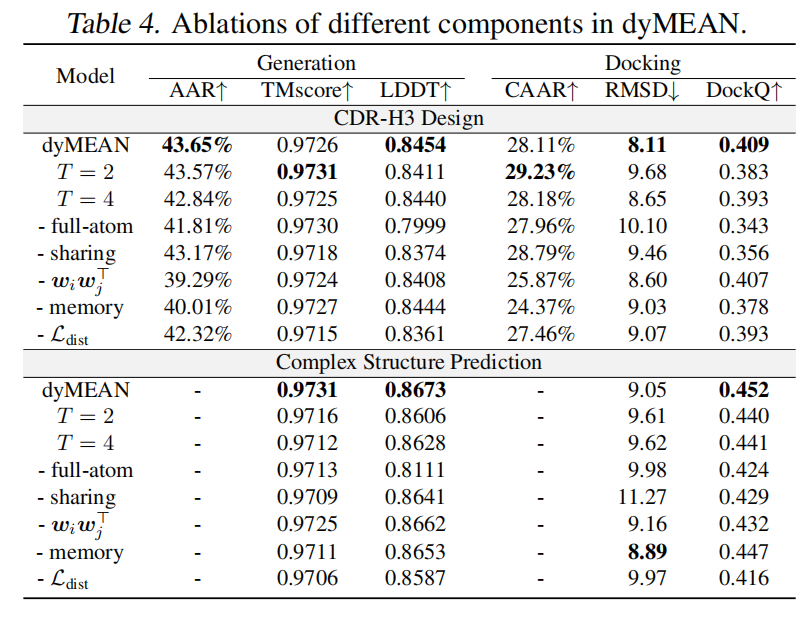
研究者对 dyMEAN 进行了消融实验,以分析各组件的贡献。
📌 实验结果(Table 4)
- T 主要影响 docking 性能,T=3 是最优选择。
- 移除全原子建模后,整体性能大幅下降,表明 侧链构象在建模中至关重要。
- 移除影子互补位共享后,所有指标(除了 CAAR)均明显下降,表明该机制对结构生成和 docking 至关重要。
- 去除可学习通道权重后,模型表现下降,表明通道权重类似于注意力机制(attention),对不同通道信息赋予不同的重要性。
- 记忆机制对 CDR-H3 设计有帮助,但对复合物结构预测影响较小,因为 CDR-H3 生成时,隐状态受记忆机制影响较大,而 3D 坐标则直接传播。
- $L_{dist}$ 对 docking 任务至关重要,研究者推测仅靠坐标无法在早期迭代正确恢复影子互补位的结构
Multiple CDRs Design and Full Antibody Design
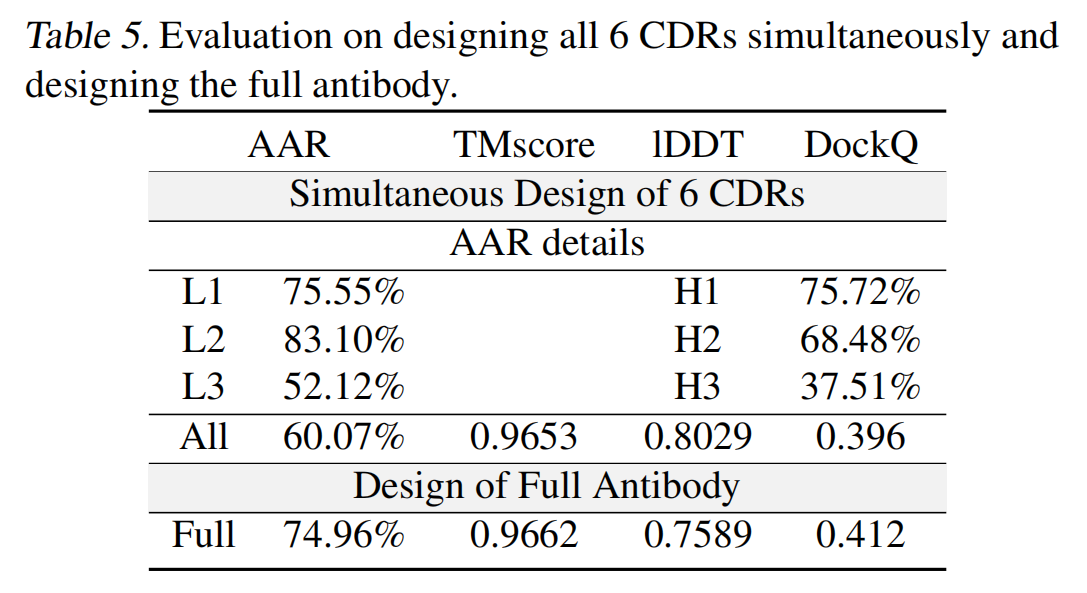
多个 CDR 设计(Multiple CDRs Design):在 CDR-H1、H2、H3 和 L1、L2、L3 全部 masked 的情况下进行生成。
完整抗体设计(Full Antibody Design):生成 包括框架区(Framework Regions, FRs)在内的完整抗体。
Limitations
Data Diversity and Evaluation Metrics
目前,深度生成模型在抗体设计任务中仍然面临挑战,其中 抗原-抗体数据的多样性不足 是主要问题之一。
研究者分析了训练集中 CDR-H3 每个位置最常见的单字母氨基酸模式,并对其从 两端向中间匹配,发现了一个 高频模式 “ARDG***DY”,其中大部分 “*” 位置都是 Y。
-
使用该单字母模式在测试集中计算 AAR,得到:AAR = 39.61%,CAAR = 26.57%
-
这表明:无意义的 unigram 模式在训练集和测试集中占据主导地位,可能会影响模型学习抗原-抗体相互作用的能力。
-
去除 CDR-H3 的前 4 个和后 2 个残基后,dyMEAN 的 AAR 下降至 31.76%,这表明 高频 unigram 模式影响了抗体序列预测的评估标准。
这些现象表明:
- 现有数据集可能需要增强(例如,通过实验室数据扩增,或者从更广泛的蛋白复合物中提取类似界面)。
- 现有的评估指标可能需要改进,例如:
- 排除可以通过 unigram 预测正确的残基,以减少数据偏差的影响。
- 引入更复杂的评估方法,以更准确衡量抗体-抗原相互作用的合理性。
Reliability of Computational Energy Functions
最终,抗体的结合亲和力(binding affinity)决定了生成的候选抗体是否具有实际价值。本研究中,dyMEAN 采用 深度学习预测器计算 ΔΔG(结合自由能变化) 作为亲和力的度量方式。然而,研究者指出当前计算能量函数仍存在以下问题:
基于统计的能量计算方法:FoldX (Schymkowitz et al., 2005),Rosetta (Alford et al., 2017),Docking 软件中的打分函数(Goodsell et al., 1996)
问题与挑战
- 这些计算能量函数的 可靠性仍然存在不确定性,其中一些方法已知与实验结果的相关性较低(Ramírez & Caballero, 2016, 2018)。
- 研究者提出了两个关键问题:
- 这些能量函数是否能够区分结合能力较弱的复合物?
- 这些能量函数(通常基于天然复合物数据训练)是否能够推广到深度学习生成的复合物?(即,深度学习模型可能会生成具有不同统计分布的复合物,而计算能量函数未必适用)
结论
- 如果没有可靠的计算能量函数,抗体设计仍然需要湿实验评估(wet-lab evaluation),然而这会 增加成本和时间开销。
- 未来的研究需要开发更具泛化性的亲和力预测器,以提高深度学习驱动的抗体设计的可靠


