FlowMatching:固定条件概率路径的向量场训练CNF
Abstract
Flow Matching 是一种新的训练CNF的方法,通过回归固定条件概率路径的向量场来进行训练。这种方法可以使用广义的高斯概率路径来进行数据样本与噪声之间的转换,从而拓展了现有扩散模型(Diffusion Models)的范畴。使用FM与扩散路径相比,实验表明其训练过程更加稳定和鲁棒,并且效果更好,尤其在生成图像时,能够获得更高的样本质量和更准确的似然估计。FM还允许使用其他非扩散概率路径进行训练,例如**最优传输(Optimal Transport,OT)**路径。使用OT路径相比于扩散路径,训练速度更快,采样效率更高,并且能实现更好的泛化能力。实验结果显示,FM框架在ImageNet数据集上表现出色,尤其在样本生成和训练效率方面优于传统的扩散方法。最后,FM方法能够通过现成的数值常微分方程(ODE)求解器进行快速、可靠的样本生成,展现了其优越的计算效率。
Introduction
扩散模型因其 训练稳定性 和 高质量样本 受到广泛关注。然而,它们依赖于固定的扩散过程,所有样本必须遵循相同的扩散路径,这导致训练和推理的灵活性受限,并导致训练时间较长,需要额外优化方法提升采样效率。
论文提出了连续归一化流(Continuous Normalizing Flows, CNFs) 作为更一般化的生成建模框架。
- CNFs 的优势
- 可以建模任意的概率路径,包括扩散模型的路径。
- 通过学习一个时间相关的向量场 vt(x)v_t(x)vt(x),数据可以流动到目标分布,而不是仅限于固定的扩散过程。
- CNFs 的挑战
- 传统最大似然训练(MLE)计算成本高,需要昂贵的数值 ODE(常微分方程)求解。
- 现有的无模拟(simulation-free)方法有缺陷:依赖于难以计算的积分(Rozen et al., 2021)。梯度估计存在偏差(Ben-Hamu et al., 2022)。
Flow Matching (FM) 方法被提出,旨在提供更高效、更稳定的 CNF 训练方式。
Preliminaries: Continuous Normalizing Flows
Continuous Normalizing Flows (CNFs) 是标准归一化流(Normalizing Flows, NFs)的连续时间版本。CNFs 能够建模任意的概率路径(Probability Path),其中也包括扩散过程(Diffusion Processes)
在 CNF 设定下:
-
数据点 $x$ 是连续流动的,满足常微分方程(ODE):
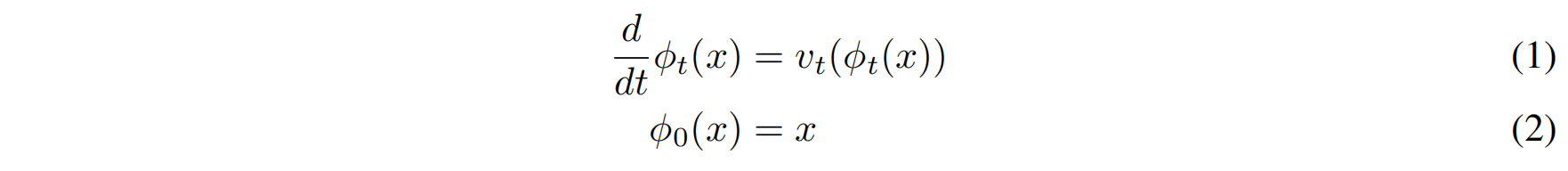
其中:
- $\phi_t(x)$ 是 CNF 变换路径(flow)。
- $v_t(x)$ 是一个时间相关的向量场,控制数据如何演化。
-
CNFs 的核心思想是:
- 利用 ODE 变换数据点,从一个简单的初始分布 $p_0(x)$ 演化到目标分布 $p_1(x)$。
- 这种变换可以由神经网络建模,形成一个参数化的向量场 $v_t(x, \theta)$,其中 $\theta$ 是神经网络参数
假设数据点 x 服从一个随时间变化的概率密度 $p_t(x)$,那么 CNF 使得概率密度在时间 ttt 发生变换,满足以下推流方程(push-forward equation):
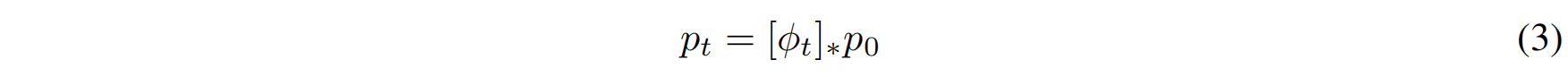
其中,推流算子(push-forward operator) $[\phi_t]_*$ 定义为:
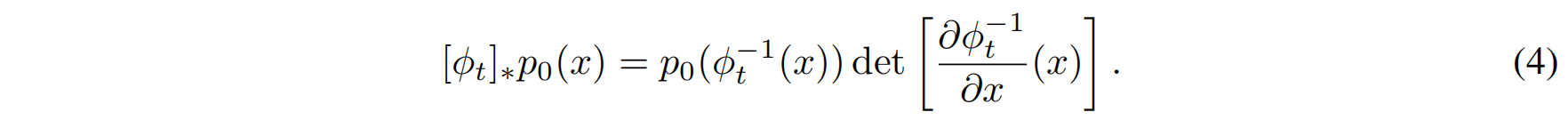
该方程表示:数据分布 $p_0(x)$ 经过 CNF 变换后,在时间 $t$ 演化为 $p_t(x)$
Flow Matching
在 CNF 中,我们希望训练一个向量场 $v_t(x)$,使其能够通过一个 概率密度路径 $p_t(x)$ 从一个初始分布 $p_0(x)$(如高斯噪声)平滑地变换为目标分布 $p_1(x)$(即数据分布)。
给定一个目标概率路径 $p_t(x)$ 和其生成向量场 $u_t(x)$,我们定义 Flow Matching(FM)目标函数 为:
$$
L_{FM}(\theta) = \mathbb{E}_{t, p_t(x)} \left[ | v_t(x) - u_t(x) |^2 \right]
$$
- 其中,$\theta$ 是可学习参数,即 CNF 的神经网络参数。
- 期望值是关于:
- 时间 $t \sim U[0,1]$ 采样的(均匀分布)。
- 数据点 $x \sim p_t(x)$ 采样的。
- 目标:让 CNF 学习到一个向量场 $v_t(x)$,使其尽可能逼近目标向量场 $u_t(x)$。
但问题在于:
- 我们通常 不知道 如何直接构造合适的 $p_t(x)$ 和 $u_t(x)$。
- 我们需要 更简单的方式 来构建这些路径,并提供一种易计算的训练目标。
Constructing $p_t$, $u_t$ From Conditional Probability Paths and Vector Fields
条件路径 $p_t(x | x_1)$
首先,我们考虑 条件路径 $p_t(x | x_1)$,即在给定某个数据点 $x_1$ 的情况下,从噪声到该数据点的转化过程。具体地,给定一个数据点 $x_1$,我们可以定义一个路径,从标准高斯噪声($p_0(x)$)到以 $x_1$ 为中心的分布($p_1(x)$)。这个过程被称为条件路径,它描述了从噪声到目标数据的演化过程。
边际化得到 $p_t(x)$
然而,我们并不是只关心单个数据点 $x_1$,而是希望得到整个数据集的转化路径。为了从 每个数据点的条件路径 得到 整体数据分布的目标路径 $p_t(x)$,我们需要对所有的条件路径进行 边际化(marginalization)。边际化的意思是把每个条件路径按照该数据点在整体数据分布中的权重加权,然后求得一个总体的路径。
这可以通过以下公式实现:
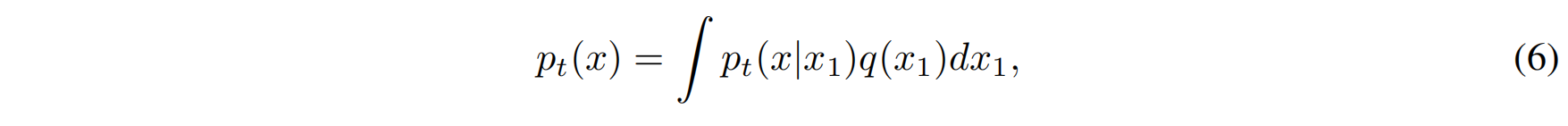
- $p_t(x | x_1)$:是给定数据点 $x_1$ 时,从噪声到 $x_1$ 的条件路径。
- $q(x_1)$:是数据分布 $q(x_1)$,即每个数据点 $x_1$ 在数据集中的出现概率。
- $p_t(x)$:是我们最终想得到的目标路径,它是所有条件路径 $p_t(x | x_1)$ 的加权平均。
通过这个过程,边际化 就是通过所有条件路径 $p_t(x | x_1)$,按每个数据点 $x_1$ 出现的概率 $q(x_1)$ 加权平均,得到一个适用于所有数据的目标路径 $p_t(x)$。
特别是在时间 $t = 1$,边际概率 $p_1$ 是一个近似于数据分布 $q$ 的混合分布:
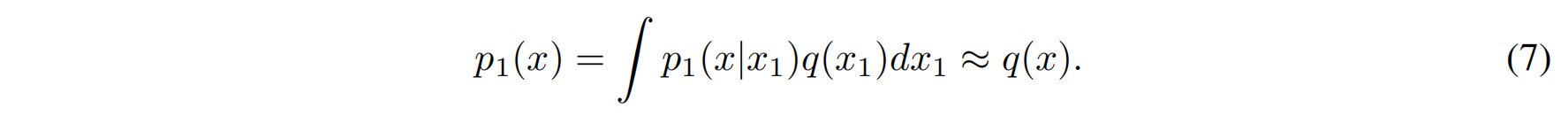
条件向量场 $u_t(x | x_1)$
接下来,我们需要构造目标 向量场 $u_t(x)$,这个向量场描述了从噪声到目标数据的演化过程。与条件路径一样,条件向量场 $u_t(x | x_1)$描述了在给定某个数据点 $x_1$ 时,从噪声到 $x_1$ 的演化过程。换句话说,给定一个数据点 $x_1$,我们可以得到一个 条件向量场,它描述了如何通过时间变化把噪声转变成 $x_1$。
边际化得到 $u_t(x)$
但是,我们并不只关心单一数据点的转化过程,而是想得到适用于所有数据点的 目标向量场 $u_t(x)$。为了实现这一点,我们需要将每个条件向量场 $u_t(x | x_1)$ 通过边际化得到总体的目标向量场。
通过边际化,我们按照数据点 $x_1$ 的出现概率 $q(x_1)$,对每个条件向量场 $u_t(x | x_1)$ 进行加权求和,从而得到一个适用于所有数据点的目标向量场 $u_t(x)$。
边际化的公式如下:
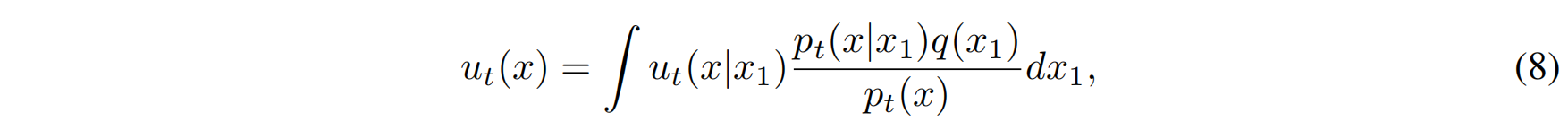
- $u_t(x | x_1)$:是给定数据点 $x_1$ 时,从噪声到 $x_1$ 的条件向量场。
- $p_t(x | x_1)$:是给定数据点 $x_1$ 时的条件路径。
- $q(x_1)$:是数据分布 $q(x_1)$,即每个数据点 $x_1$ 在数据集中的出现概率。
- $p_t(x)$:是目标概率路径,它是所有条件路径的加权平均。
- $u_t(x)$:是最终得到的目标向量场,它是所有条件向量场的加权平均。
论文中的 定理 1 证明了:如果条件向量场 $u_t(x | x_1)$ 生成了条件概率路径 $p_t(x | x_1)$,那么 边际向量场 $u_t(x)$ 也能生成边际概率路径 $p_t(x)$。
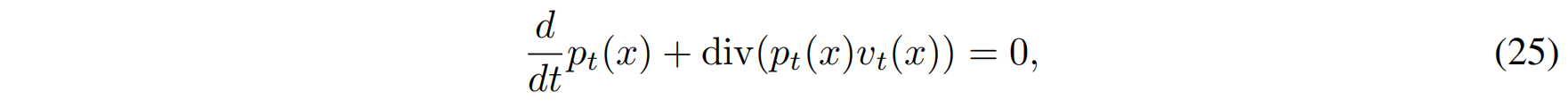

Conditional Flow Matching
一个实际问题是,直接计算目标向量场 ut(x)u_t(x)ut(x) 仍然是不可行的,因为它涉及计算复杂的边际积分(即对所有数据点进行加权求和)。
所以,**我们希望找到一种方法,使得我们不需要直接计算 $u_t(x)$,但仍然能训练出正确的向量场 $v_t(x)$。**这就是 条件流匹配(Conditional Flow Matching, CFM) 的核心思想。
我们先回顾一下 Flow Matching (FM) 目标函数,它的形式如下:
$$
L_{FM}(\theta) = \mathbb{E}_{t, p_t(x)} \left[ | v_t(x) - u_t(x) |^2 \right]
$$
- 这里 $v_t(x)$ 是 CNF 的神经网络 预测的向量场(带有可训练参数 θ\thetaθ)。
- $u_t(x)$ 是 目标向量场(但它很难计算)。
- 我们的目标是让 $v_t(x)$ 尽可能匹配 $u_t(x)$,即最小化二者的均方误差(MSE)。
- 但问题是:$u_t(x)$ 需要边际化计算,它涉及复杂的积分,无法直接求解!
于是,我们需要一个 替代方案 —— 条件流匹配(CFM)。
CFM 目标函数如下:
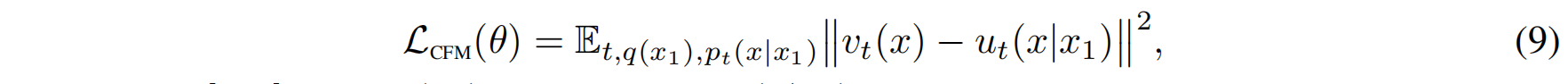
与 FM 目标函数相比:
- CFM 不直接涉及 $)u_t(x)$,而是用 $u_t(x | x_1)$ 替代它。
- CFM 只需要采样 $x_1$ 和 $x$,不需要计算复杂的边际积分!
CFM 的直觉理解:
- FM 目标函数要求模型直接匹配目标向量场 $u_t(x)$,但计算这个 $u_t(x)$ 很难。
- CFM 让我们不去计算全局目标向量场 $u_t(x)$,而是仅仅匹配局部的条件向量场 $u_t(x | x_1)$。
- 这样做的好处是,我们可以通过数据采样直接计算 CFM 目标,而不需要计算复杂的积分!
虽然 CFM 目标函数看起来和 FM 不一样,但论文的定理 2 证明了它们在梯度上的等价性:
$$
\nabla_{\theta} L_{FM}(\theta) = \nabla_{\theta} L_{CFM}(\theta)
$$
换句话说,优化 CFM 目标函数,与优化 FM 目标函数是等效的,但 CFM 更易计算。
为什么它们是等价的? 回顾 FM 目标:
$$
L_{FM}(\theta) = \mathbb{E}{t, p_t(x)} \left[ | v_t(x) - u_t(x) |^2 \right]
$$
其中,$u_t(x)$ 是通过边际化得到的:
$$
u_t(x) = \int u_t(x | x_1) \frac{p_t(x | x_1) q(x_1)}{p_t(x)} dx_1
$$
如果把这个 $u_t(x)$ 代入 FM 目标函数,我们得到:
$$
L{FM}(\theta) = \mathbb{E}{t, p_t(x)} \left[ | v_t(x) - \int u_t(x | x_1) \frac{p_t(x | x_1) q(x_1)}{p_t(x)} dx_1 |^2 \right]
$$
在数学上,我们可以证明 直接优化这个目标,等价于 优化 CFM 目标,即:
$$
L{CFM}(\theta) = \mathbb{E}_{t, q(x_1), p_t(x | x_1)} \left[ | v_t(x) - u_t(x | x_1) |^2 \right]
$$
直观来说:
- FM 需要计算复杂的积分,而 CFM 只需要简单地采样。
- 它们的梯度是一样的,因此训练效果相同。

Conditional Probability Paths and Vector Fields
我们考虑构造 高斯条件概率路径(Gaussian conditional probability path),其形式如下:
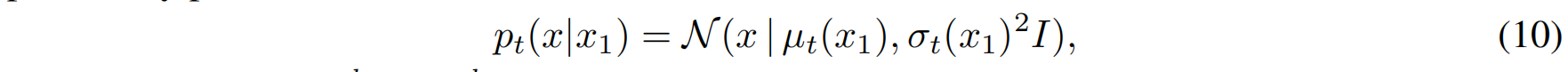
其中:
- $\mu_t(x_1)$ 是随时间 $t$ 变化的均值函数,决定了数据点的漂移轨迹;
- $\sigma_t(x_1)$ 是随时间 $t$ 变化的标准差,控制路径的不确定性。
为了确保所有路径在 $t = 0$ 处收敛到一个已知的高斯分布(如标准高斯分布),而在 $t = 1$ 处收敛到数据点 $x_1$,我们设定:
-
初始条件(t = 0):
$$
\mu_0(x_1) = 0, \quad \sigma_0(x_1) = 1
$$
这样所有路径的起点都位于标准高斯分布 $p(x) = \mathcal{N}(x | 0, I)$。 -
终止条件(t = 1):
$$
\mu_1(x_1) = x_1, \quad \sigma_1(x_1) = \sigma_{\min}
$$
其中 $\sigma_{\min}$ 是一个较小的数值,使得 $p_1(x | x_1)$ 在 $x_1$ 附近高度集中,从而近似目标分布 $q(x)$。
向量场 $u_t(x | x_1)$ 决定了数据点 $x$ 在时间 $t$ 处的流动方向。
这里,我们采用 高斯分布的标准变换(canonical transformation) 来构造向量场。定义一个变换:
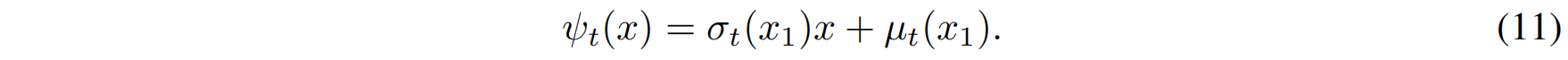
当 $x$ 服从标准高斯分布时,该变换将其映射到均值 $\mu_t(x_1)$ 和标准差 $\sigma_t(x_1)$ 的高斯分布,即:
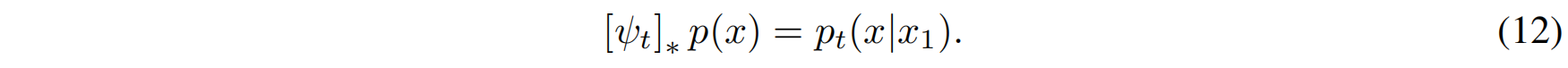
这里 $[\psi_t]_*$ 表示概率分布的推前变换(push-forward)。接着,利用普通微分方程:
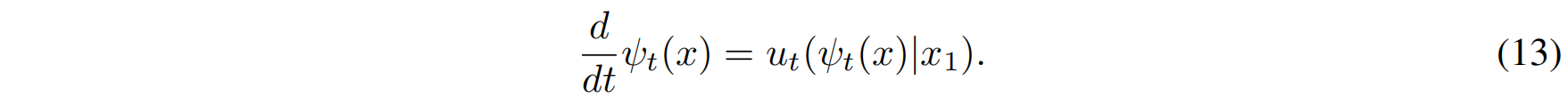
我们可以得到向量场 $u_t(x | x_1)$ 的解析表达式:
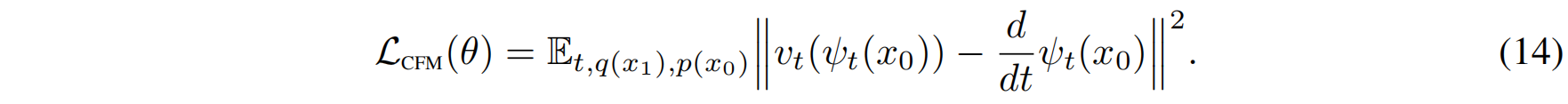
这一结果意味着:
- 第一项 $\frac{\sigma_t’}{\sigma_t} (x - \mu_t)$ 控制向量场的缩放和拉伸;
- 第二项 $\mu_t’$ 直接决定了漂移的方向。

Special Instances of Gaussian Conditional Probability Paths
Example I: Diffusion conditional VFs
扩散模型(Diffusion Models)是一类生成模型,它们通过在数据点上逐步添加噪声,直到数据点近似纯噪声(即标准高斯分布)来进行建模。这些扩散过程可以被视为随机过程(Stochastic Processes),并且它们需要满足严格的数学约束,以便在任意时间 ttt 处能够获得封闭形式(closed-form)的表示。
在 Flow Matching 框架下,我们可以使用 高斯条件概率路径(Gaussian Conditional Probability Paths):
$$
p_t(x | x_1) = \mathcal{N} (x | \mu_t(x_1), \sigma_t^2(x_1) I)
$$
其中:
- $\mu_t(x_1)$ 是均值函数,控制数据点如何随时间漂移;
- $\sigma_t(x_1)$ 是标准差函数,控制数据点的不确定性如何变化。
以下介绍两种常见的扩散路径:
- 反向 Variance Exploding (VE) 扩散路径。
- 反向 Variance Preserving (VP) 扩散路径。
在 VE 扩散模型中:
- 正向过程(Forward Process, Data → Noise):从数据点 x1x_1x1 开始,逐渐添加噪声,最终变为纯噪声。
- 反向过程(Reverse Process, Noise → Data):从噪声点 xxx 开始,逐渐去除噪声,最终生成符合数据分布的样本。
VE 扩散路径的条件概率分布定义为:
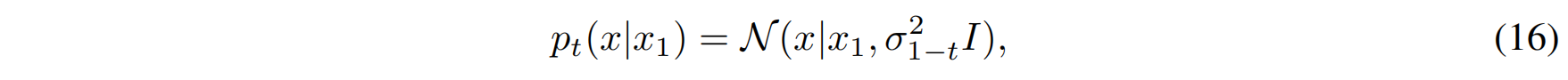
其中:
- $\sigma_t$ 是随时间递增的函数;
- 设定初始条件: $\sigma_0 = 0, \quad \sigma_1 \gg 1$ 这表示在 $t=0$ 时,数据点没有噪声,而在 $t=1$ 时,数据点变为纯噪声。
根据该概率路径:
- 均值函数: $\mu_t(x_1) = x_1$
- 标准差函数: $\sigma_t(x_1) = \sigma_{1-t}$
代入 Theorem 3 的向量场公式:
$$
u_t(x | x_1) = \frac{\sigma_t’(x_1)}{\sigma_t(x_1)} (x - \mu_t(x_1)) + \mu_t’(x_1)
$$
由于 $\mu_t(x_1) = x_1$ 是常数,求导后 $\mu_t’(x_1) = 0$,所以:
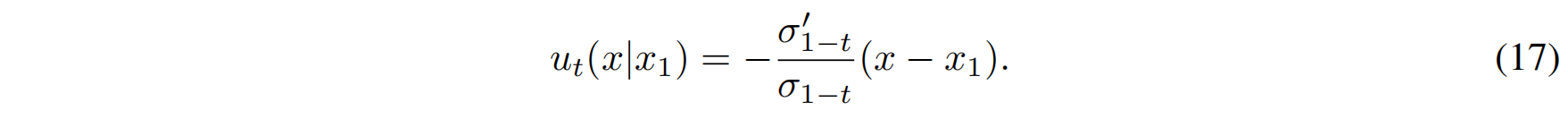
Variance Preserving (VP) 扩散路径
VP 扩散模型的特点:
- 正向过程(Forward Process, Data → Noise):数据点均值缩小,噪声逐渐增加。
- 反向过程(Reverse Process, Noise → Data):数据点均值逐渐恢复到 x1x_1x1,同时噪声减少。
VP 扩散路径的条件概率分布定义为:
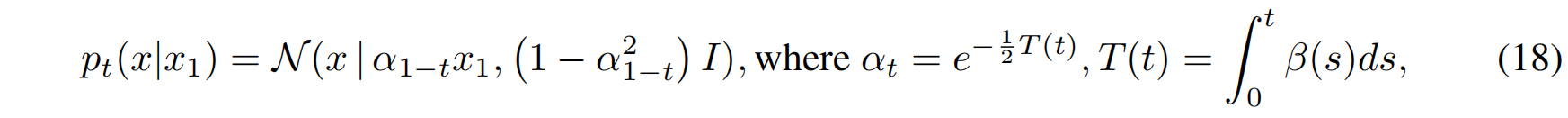
其中:
- $\alpha_t$ 是控制均值衰减的因子,$T(t) $ 是累积噪声函数,$\beta(s)$ 是噪声尺度函数(Noise Scale Function)。
计算向量场
- 均值函数: $\mu_t(x_1) = \alpha_{1-t} x_1$
- 标准差函数: $\sigma_t(x_1) = \sqrt{1 - \alpha^2_{1-t}}$
代入 Theorem 3 提供的向量场公式:
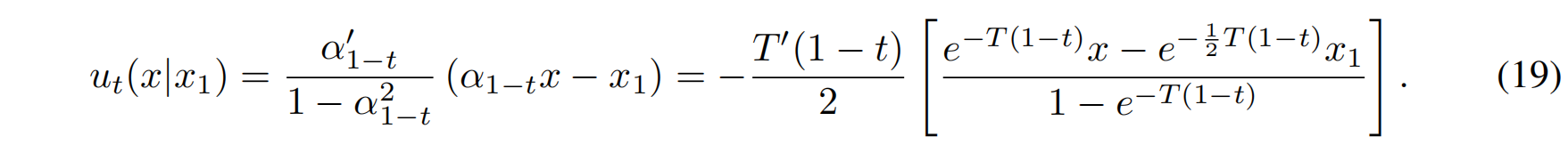
Example II: Optimal Transport conditional VFs
在最优传输的框架下,一个更自然的选择是 让均值和标准差随时间线性变化:
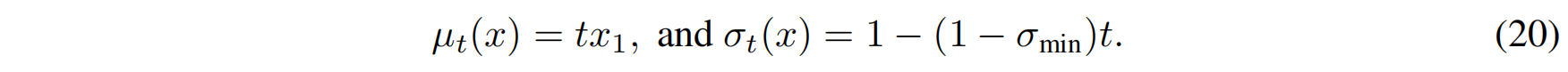
- 均值 $\mu_t(x)$) 线性变化,意味着数据点沿着直线逐步靠近 $x_1$。
- 标准差 $\sigma_t(x)$ 逐渐减少,确保数据点在靠近 $x_1$ 时更稳定。
根据 Theorem 3 提供的向量场公式:
$$
u_t(x | x_1) = \frac{\sigma_t’(x_1)}{\sigma_t(x_1)} (x - \mu_t(x_1)) + \mu_t’(x_1)
$$
对 $\mu_t(x) = t x_1$ 和 $\sigma_t(x) = 1 - (1 - \sigma_{\min})t$ 计算导数:
- 均值导数: $\mu_t’(x_1) = x_1.$
- 标准差导数: $\sigma_t’(x_1) = -(1 - \sigma_{\min}).$
代入 Theorem 3:
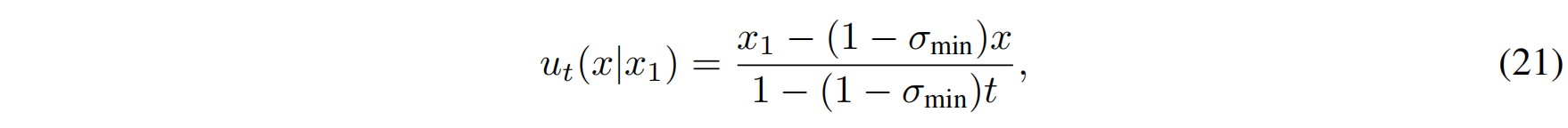
OT 方法的核心思想是 让数据点沿着最优路径流动。因此,对应的 流动映射(Flow Map) 设定为:
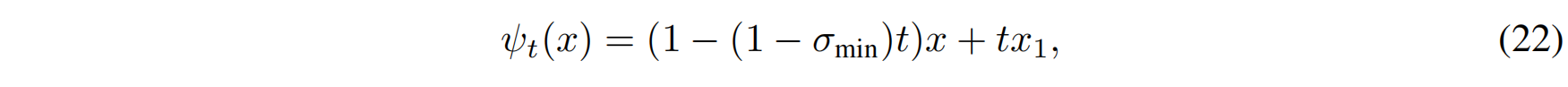
这表示:
- 数据点 $x$ 逐渐收缩到目标点 $x_1$,并且流动轨迹是直线。
- 数据点的变换是仿射的(Affine),这简化了模型的学习任务。
在 Flow Matching 框架下,损失函数(CFM Loss)变为:
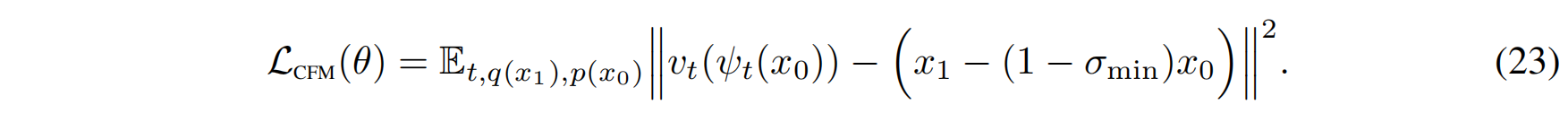
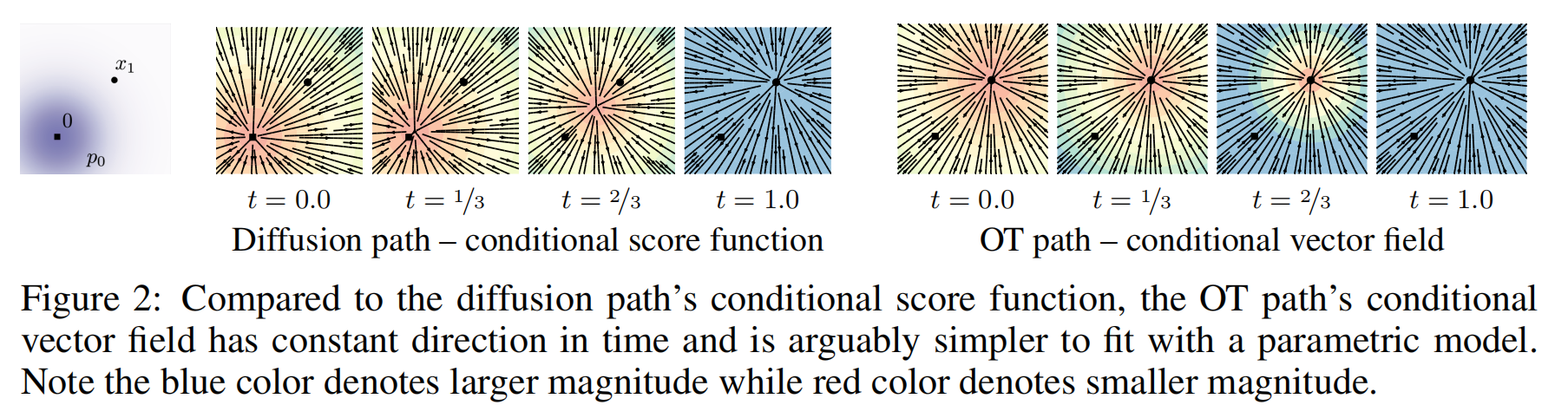
论文提供的可视化结果(Figure 3)展示了:
- 扩散路径的轨迹是曲线,在靠近目标数据点时可能会有震荡(oscillations)。
- OT 轨迹是直线,数据点始终朝着目标点前进,没有额外的回溯。
Experiments
Density Modeling and Sample Quality on ImageNet
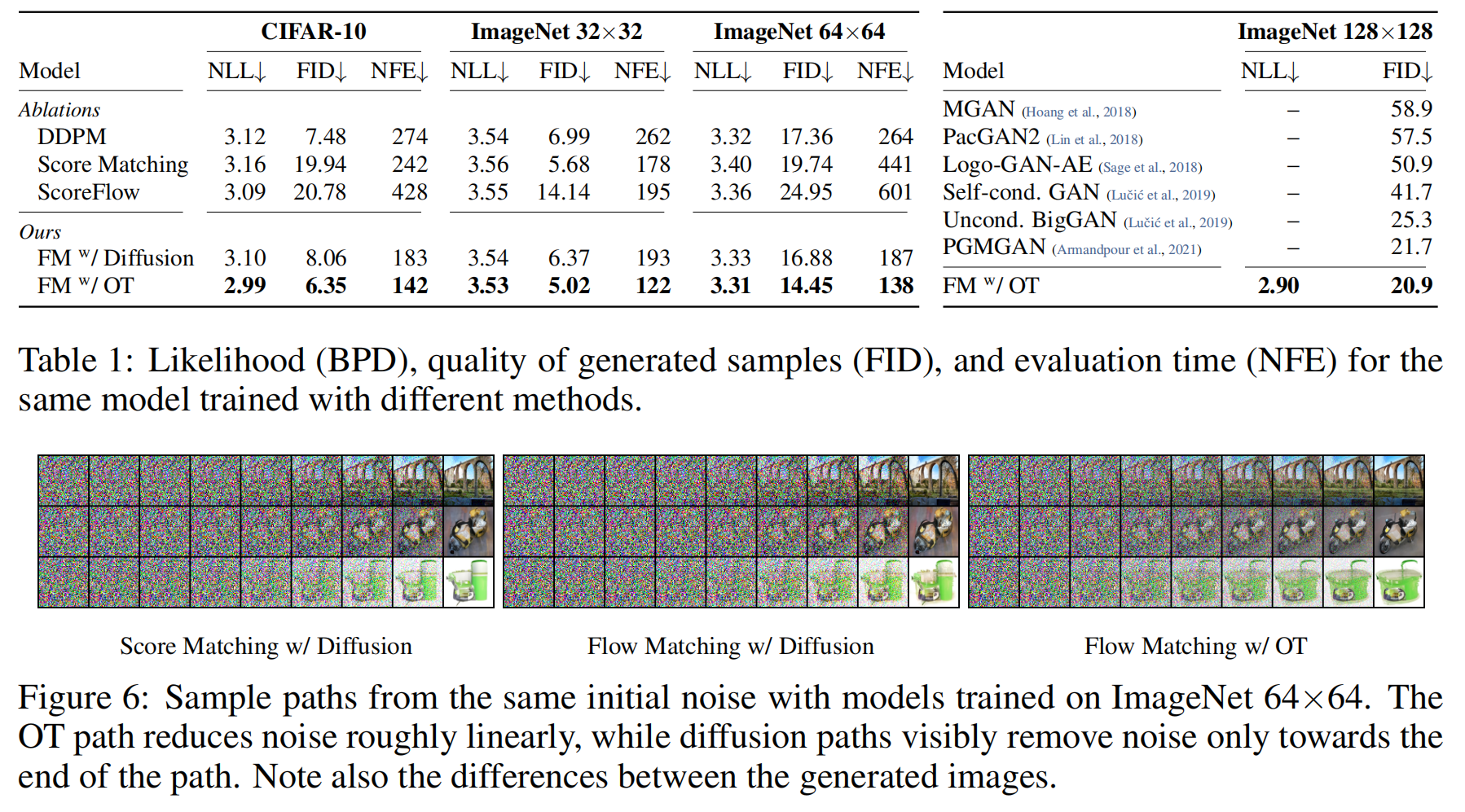
这一部分研究了 Flow Matching (FM) 在图像生成任务上的表现,并与 DDPM、Score Matching、ScoreFlow 进行对比。主要实验指标包括:
- NLL(Negative Log-Likelihood, 负对数似然):衡量模型生成数据的概率。
- FID(Fréchet Inception Distance):衡量生成样本与真实数据分布的相似性(越低越好)。
- NFE(Number of Function Evaluations):衡量生成样本所需的计算复杂度(越低越好)。
- Flow Matching (FM) 方法相较于 DDPM、Score Matching、ScoreFlow,能够达到更低的 FID 和 NLL:
- 在 所有数据集上,FM with OT path 取得了最佳的 FID 和 NLL,表明它生成的图像更清晰、质量更高。
- FM with OT 比 Score Matching 和 ScoreFlow 方法更稳定,因为 ScoreFlow 需要更多的采样步骤(更高的 NFE)。
- OT 路径(Optimal Transport Path)优于 Diffusion 路径:
- 在相同的 Flow Matching 框架下,OT 方法比 Diffusion 方法的 FID 更低,NFE 更少,意味着 OT 采样路径更优。
Sampling Efficiency

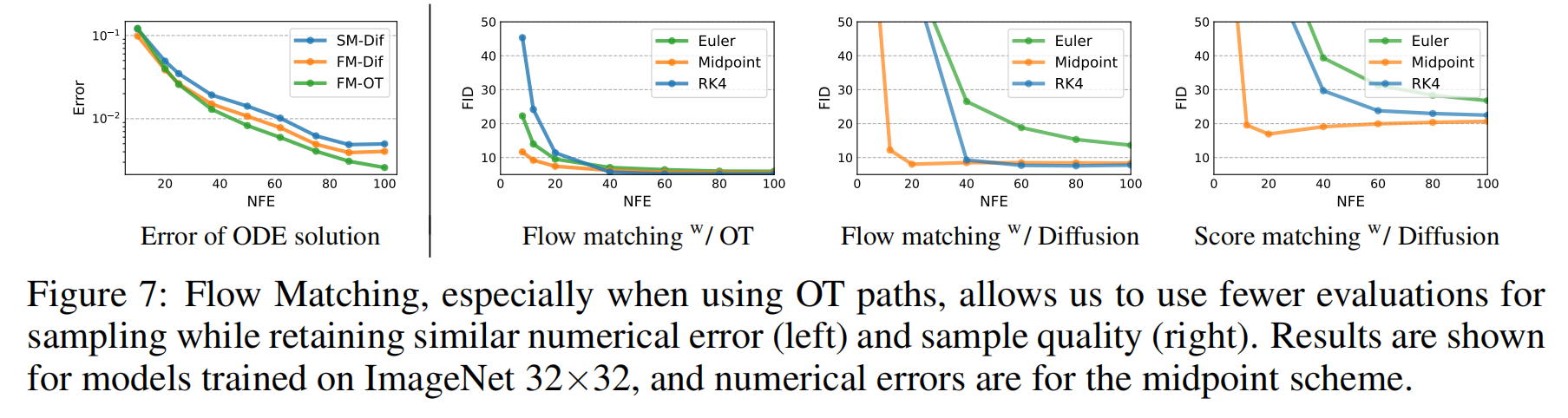
这一部分研究了 Flow Matching 在 采样效率(Sampling Efficiency) 方面的表现,即 在不同计算预算下的生成质量。
FM-OT 采样路径比扩散路径更快达到高质量样本:
- 误差分析表明,在 低计算成本(60% 计算预算)下,OT 仍然能够达到较低的误差。
- 生成的样本在 极少的 NFE 下仍然具有良好的 FID。
扩散路径(Diffusion Path)在初期仍然包含大量噪声:
- 观察 ImageNet-64 生成样本的路径:
- OT 方法能更早生成清晰图像。
- 扩散路径方法只有在最后阶段才能有效去噪。
Conditional Sampling from Low-Resolution Images
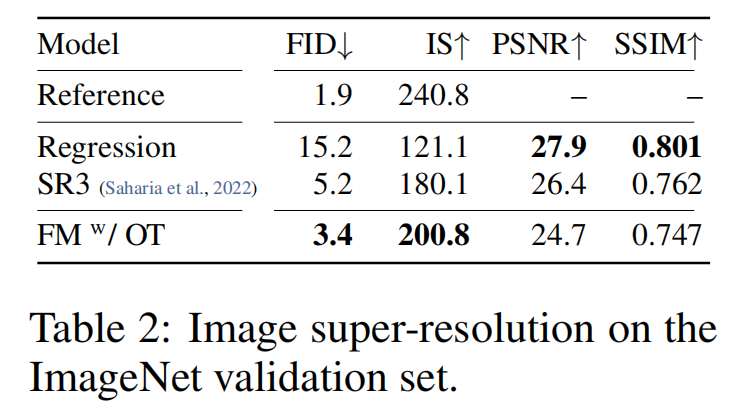
这一部分研究了 Flow Matching 在条件图像生成(Conditional Image Generation)上的应用,即:
- 超分辨率任务(Super-Resolution):从 低分辨率 64×64 图像生成 256×256 高清图像。
- 比较 Flow Matching 与其他超分辨率方法(如 SR3)。


